Simulating summary data for weak instruments

library(simulateGP)
library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr     1.1.4     ✔ readr     2.1.4
#> ✔ forcats   1.0.0     ✔ stringr   1.5.1
#> ✔ ggplot2   3.4.2     ✔ tibble    3.2.1
#> ✔ lubridate 1.9.2     ✔ tidyr     1.3.0
#> ✔ purrr     1.0.2     
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag()    masks stats::lag()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(mvtnorm)

Weak instrument bias

Useful links:

• https://web.stanford.edu/~mrosenfe/soc_meth_proj3/matrix_OLS_NYU_notes.pdf
• https://en.wikipedia.org/wiki/Instrumental_variables_estimation#Interpretation_as_two-stage_least_squares
• https://www.youtube.com/watch?v=JK-8XNIoAkI
• http://econ.lse.ac.uk/staff/spischke/ec533/Weak%20IV.pdf
• https://ocw.mit.edu/courses/economics/14-384-time-series-analysis-fall-2013/lecture-notes/MIT14_384F13_lec7and8.pdf
• https://www.nber.org/econometrics_minicourse_2018/2018si_methods.pdf
• https://www.ncbi.nlm.nih.gov/pubmed/21414999
• https://stats.stackexchange.com/questions/48366/standard-errors-for-covariance-estimate-in-r

Parameters include:

• Sample size
• Number of SNPs
• Allele frequencies of SNPs
• Heritability of the phenotype
• Effects of each SNP on the phenotype

h2 <- 0.4
nsnp <- 100
nid <- 10000

G <- make_geno(nid, nsnp, 0.5)
Gs <- scale(G)


bsim <- rnorm(nsnp, 0, sqrt(h2))

bv <- Gs %*% bsim


var(bv)
#>          [,1]
#> [1,] 43.19063
sd(bv)
#> [1] 6.571958


# h2 <- b^2 * 2 * maf * (1 - maf) / vy
# ve <- vy - vg

h2 <- 0.4
nsnp <- 100
nid <- 10000

G <- make_geno(nid, nsnp, 0.5)
b <- choose_effects(nsnp, h2)
y <- make_phen(b, G)
head(y)
#> [1] -0.3527628  1.1033438  0.7469846  0.8851455 -0.2072078  1.5914748
var(y)
#> [1] 1

bv <- G %*% b
cor(bv, y)^2
#>           [,1]
#> [1,] 0.3963762
bhat <- gwas(y, G)

btheory <- generate_gwas_ss(dplyr::tibble(beta=b, af=rep(0.5, nsnp), snp=1:nsnp), nid)
plot(btheory$beta ~ bhat$bhat)
plot(btheory$se ~ bhat$se)
plot(log10(btheory$pval) ~ log10(bhat$pval))

Standard error of beta

\[ s_{\hat{\beta}} = \sqrt{\frac{MSE}{SSX}} \]

Check that SSX is calculated correctly when using MAF to obtain var(X)

set.seed(100)
param <- expand.grid(
    af = runif(1000)/2
)
param$n <- sample(300:10000, 1000)

for(i in 1:nrow(param))
{
    g <- rbinom(param$n[i], 2, param$af[i])
    param$ssx_emp[i] <- sum((g - mean(g))^2)
    param$ssx_emp2[i] <- var(g) * (param$n[i] - 1)
    param$ssx_exp[i] <- 2 * param$af[i] * (1 - param$af[i]) * (param$n[i] - 1)
}

plot(param$ssx_emp, param$ssx_emp2)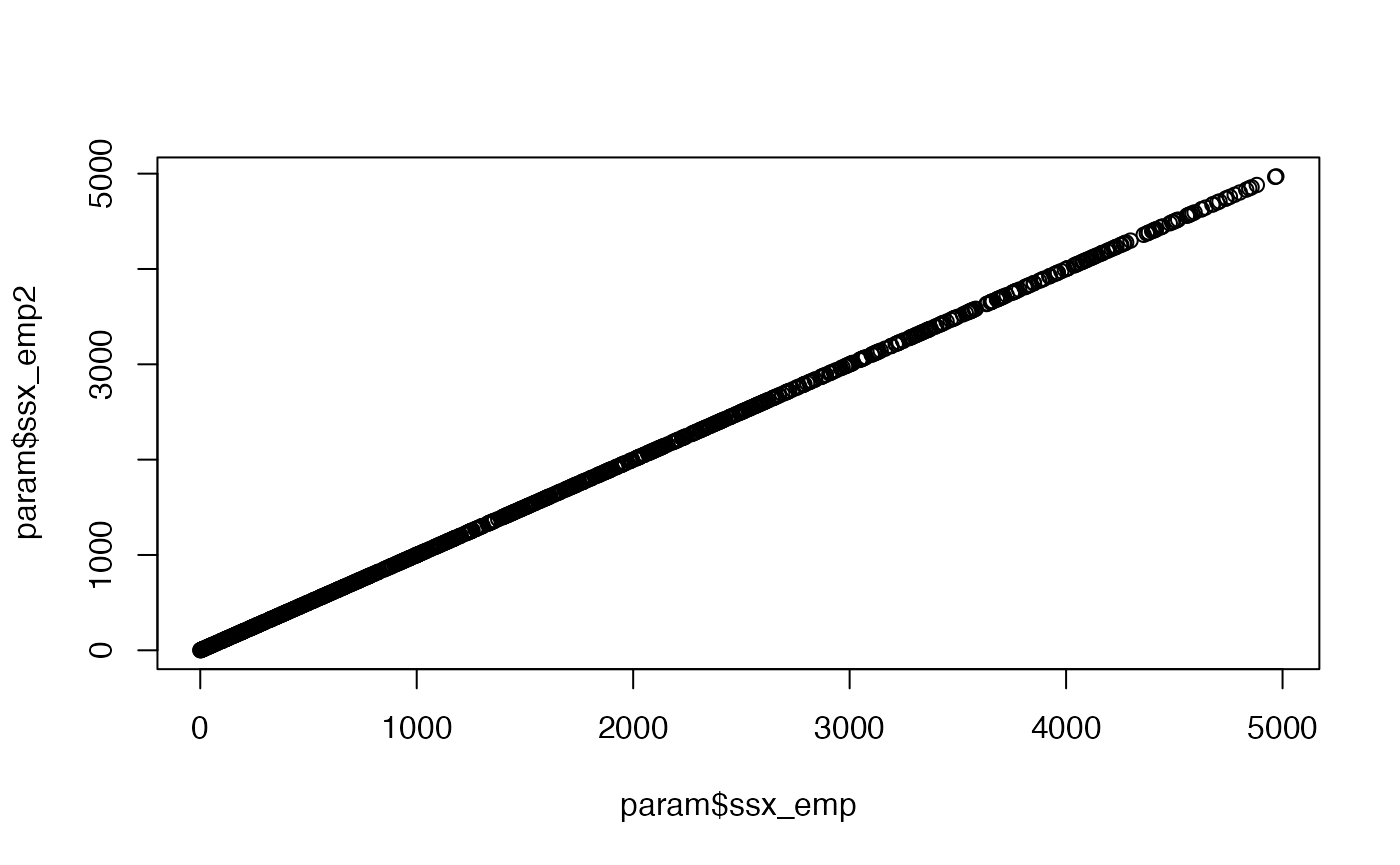

plot(param$ssx_emp, param$ssx_exp)

Now check MSE

param$b <- rnorm(nrow(param))

for(i in 1:nrow(param))
{
    g <- rbinom(param$n[i], 2, param$af[i])
    y <- g * param$b[i] + rnorm(param$n[i])
    param$vy[i] <- var(y)
    param$r2[i] <- cor(g,y)^2
    mod <- lm(y ~ g)
    param$mse[i] <- anova(mod)[[3]][2]
    param$mse_exp[i] <- expected_mse(param$b[i], param$af[i], param$vy[i])
    mod2 <- summary(mod)$coefficients
    param$bhat[i] <- mod2[2,1]
    param$se[i] <- mod2[2,2]
    param$se_theor[i] <- expected_se(param$b[i], param$af[i], param$n[i], param$vy[i])
}

plot(param$mse, param$mse_exp)

plot(param$bhat, param$b)

plot(param$se, param$se_theor)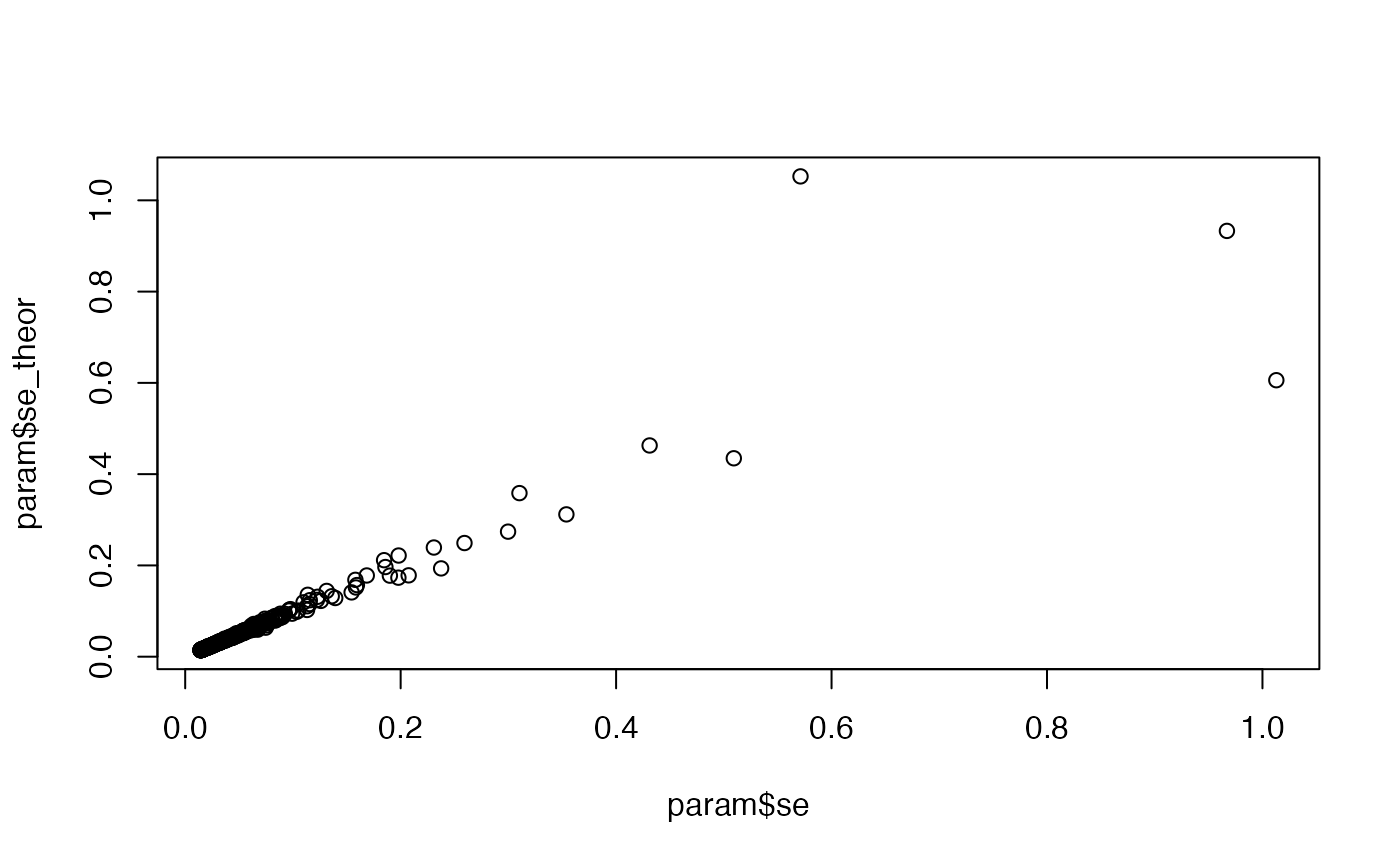

hist(param$r2)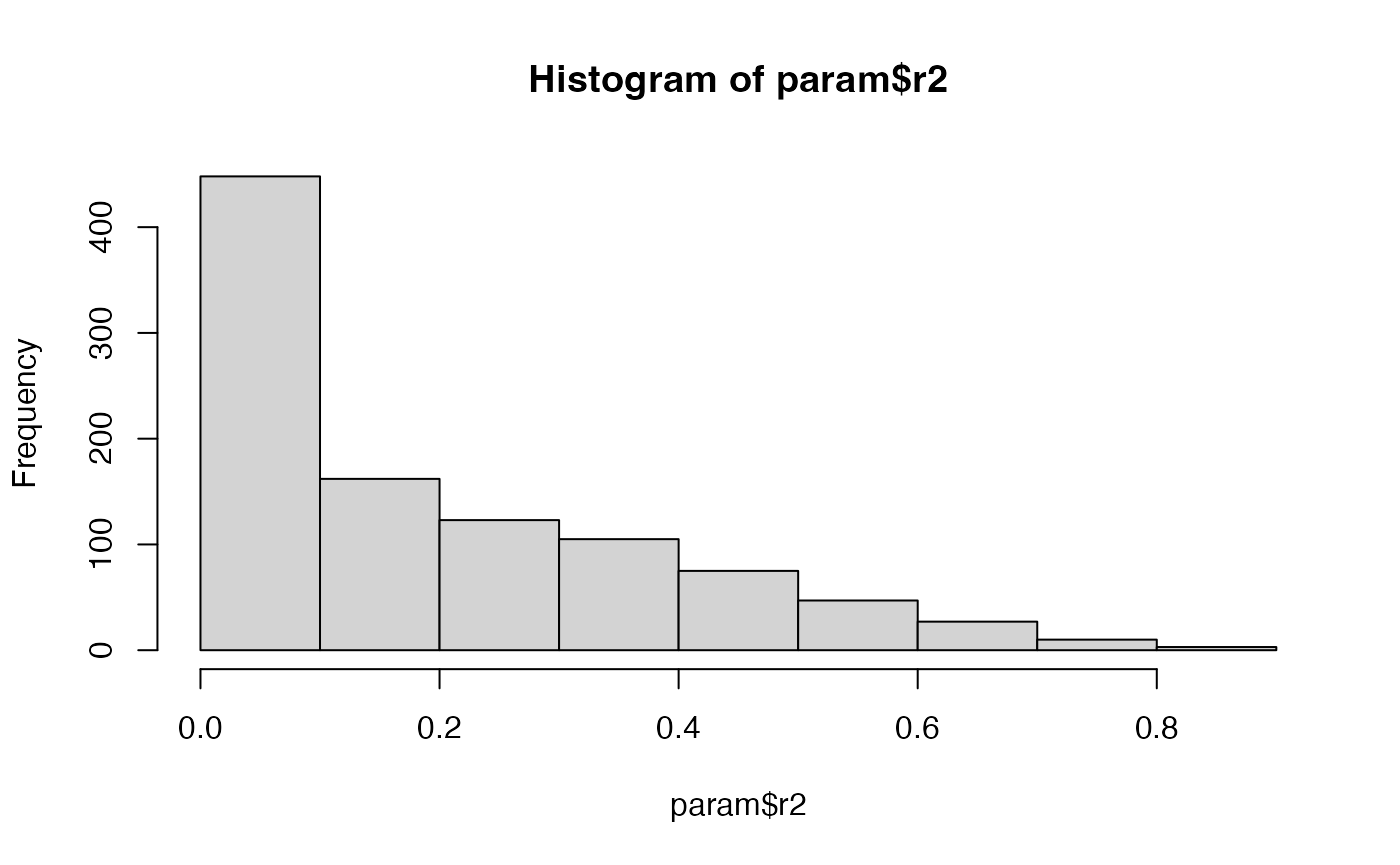

ggplot(param, aes(mse, mse_exp)) +
geom_point(aes(colour=af))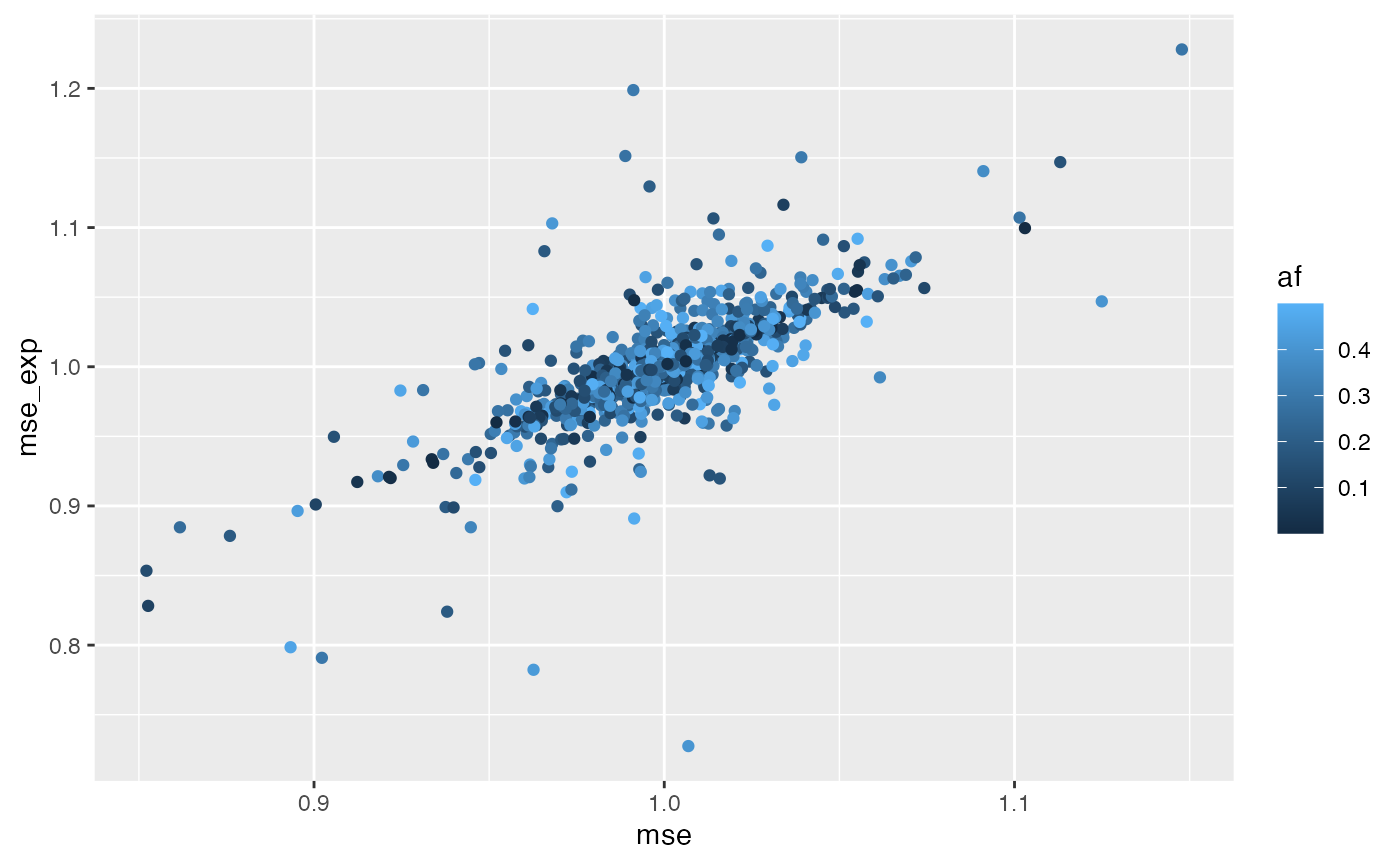

ggplot(param, aes(mse, mse_exp)) +
geom_point(aes(colour=r2))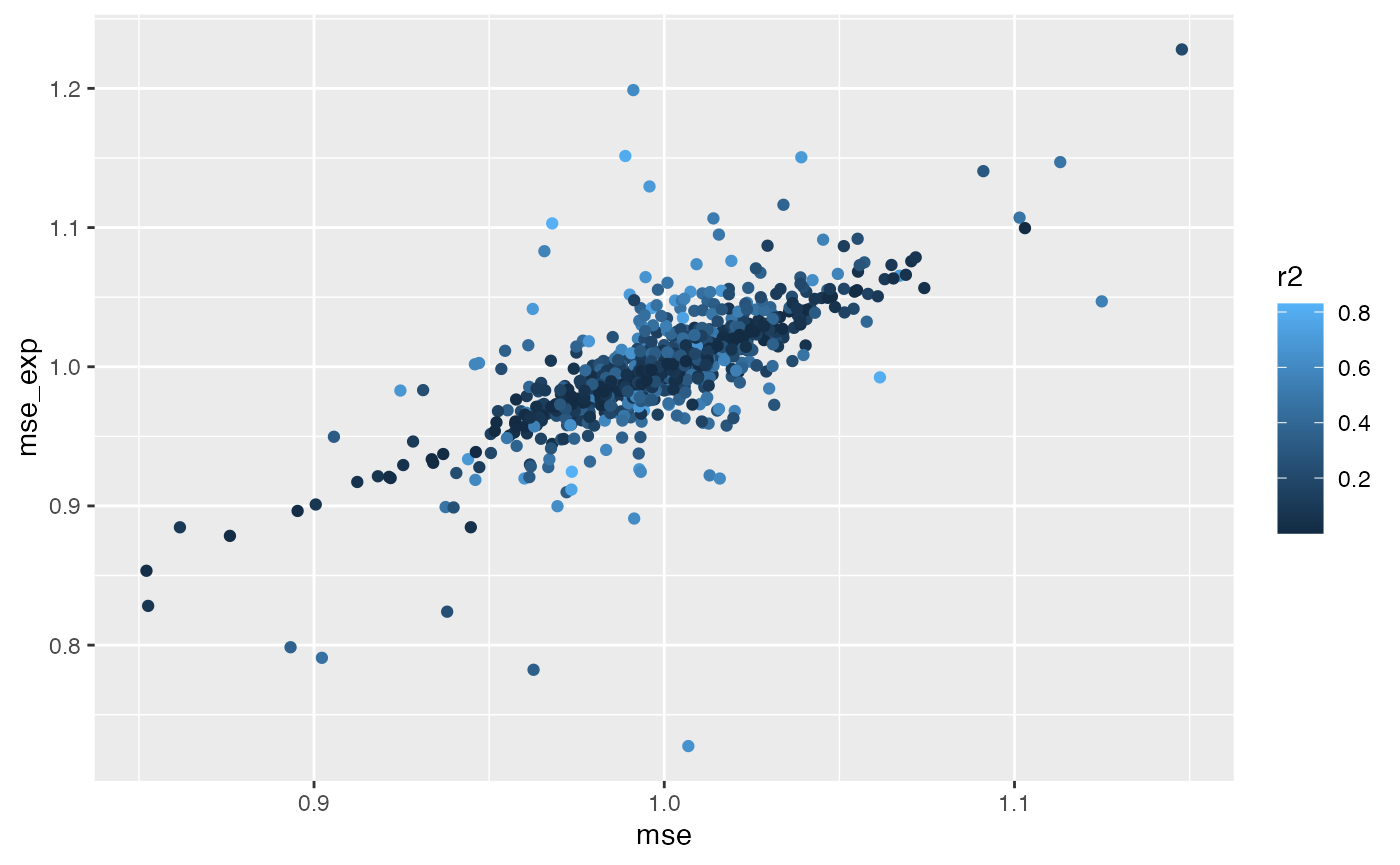

Weak instrument bias

get_biv_bias <- function(n, rho, beta, pi1)
{
    err <- mvtnorm::rmvnorm(n, c(0,0), matrix(c(1,rho,rho,1), 2, 2))
    eta <- err[,1]
    zeta <- err[,2]
    z <- rnorm(n)
    x <- pi1 * z + zeta
    y <- beta * x + eta

    Pz <- z %*% solve(t(z) %*% z) %*% t(z)

    biv <- solve(t(x) %*% Pz %*% x) %*% t(x) %*% Pz %*% y
    bias <- solve(t(x) %*% Pz %*% x) %*% t(x) %*% Pz %*% eta

    return(c(biv, bias))
}


param <- expand.grid(
    n = c(100),
    pi1=seq(0, 0.1, by=0.02),
    beta=c(0,1),
    rho=seq(0, 0.8, by=0.2),
    sim=1:200
)

dim(param)
#> [1] 12000     5
for(i in 1:nrow(param))
{
    mod <- get_biv_bias(param$n[i], param$rho[i], param$beta[i], param$pi1[i])
    param$biv[i] <- mod[1]
    param$bias[i] <- mod[2]
}

library(dplyr)
params <- group_by(param, n, pi1, beta, rho) %>%
summarise(biv=median(biv), bias=median(bias), nsim=n())
#> `summarise()` has grouped output by 'n', 'pi1', 'beta'. You can override using
#> the `.groups` argument.

ggplot(params, aes(y=bias, x=pi1, group=as.factor(rho))) +
geom_point(aes(colour=as.factor(rho))) +
geom_line(aes(colour=as.factor(rho))) +
facet_grid(n ~ beta)

n <- 1000
pi1 <- 1
beta <- 1
err <- rmvnorm(n, c(0,0), matrix(c(1,0.8,0.8,1), 2, 2))
eta <- err[,1]
zeta <- err[,2]
z <- rnorm(n)
x <- pi1 * z + zeta
y <- beta * x + eta

Pz <- z %*% solve(t(z) %*% z) %*% t(z)

biv <- solve(t(x) %*% Pz %*% x) %*% t(x) %*% Pz %*% y
bias <- solve(t(x) %*% Pz %*% x) %*% t(x) %*% Pz %*% eta

t(x) %*% x
#>          [,1]
#> [1,] 2000.966
t(x) %*% Pz %*% x
#>          [,1]
#> [1,] 988.8171

cor(x, z)^2
#> [1] 0.4944307
t(x) %*% x * cor(x,z)^2
#>          [,1]
#> [1,] 989.3389

var(x) * (length(x)-1)
#> [1] 2000.899

sum((x - mean(x))^2) / (n-1) * (n)
#> [1] 2002.902

sum(x^2)
#> [1] 2000.966

t(x) %*% x / t(x) %*% Pz %*% x
#>          [,1]
#> [1,] 2.023595

sum(z^2) / (length(z) - 1)
#> [1] 0.9957517


cov(x,y) / var(x)
#> [1] 1.408792

solve(t(x) %*% x) %*% t(x) %*% y
#>         [,1]
#> [1,] 1.40886




sum(x^2)
#> [1] 2000.966



u <- rnorm(n)
z <- rnorm(n)
x <- u * 2 + z + rnorm(n)
y <- u * -2 + x * 2 + rnorm(n)

res1 <- residuals(lm(x ~ z))
res2 <- residuals(lm(y ~ x))

cor(res1, res2)
#> [1] -0.2063041

cor(u, x)^2 * cor(y, u)^2
#> [1] 0.2032169

(x'x)-1 x'(xb + e)
(x'x)-1 x'xb + x'e

solve(t(x) %*% x) %*% t(x) %*% (x * 5 + eta)
#>          [,1]
#> [1,] 5.026537

cov(g,x) = cov(g, b1*g + a1*u + e)
= b1 var(g) + a1 cov(g, u)

cov(g,y) = cov(g, b2*x + a2*u + e)
= b2 b1 var(g) + b2 a1 cov(g, u) + a2 cov(g, u)
= b2 b1 var(g) + cov(g,u) (b2 a1 + a2)
= b2 (b1 var(g) + a1 cov(g, u)) + a2 cov(g, u)

a <- rnorm(1000)
b <- rnorm(1000)
cov(a,b)
#> [1] -0.03606378
sum((a-mean(a)) * (b - mean(b)))
#> [1] -36.02772

sum(a * b) + sum((a-mean(a))^2) * sum((b-mean(b))^2)
#> [1] 1062550

Specify

• Number of SNPs

fun <- function(nsnp, pi0, s)
{

}

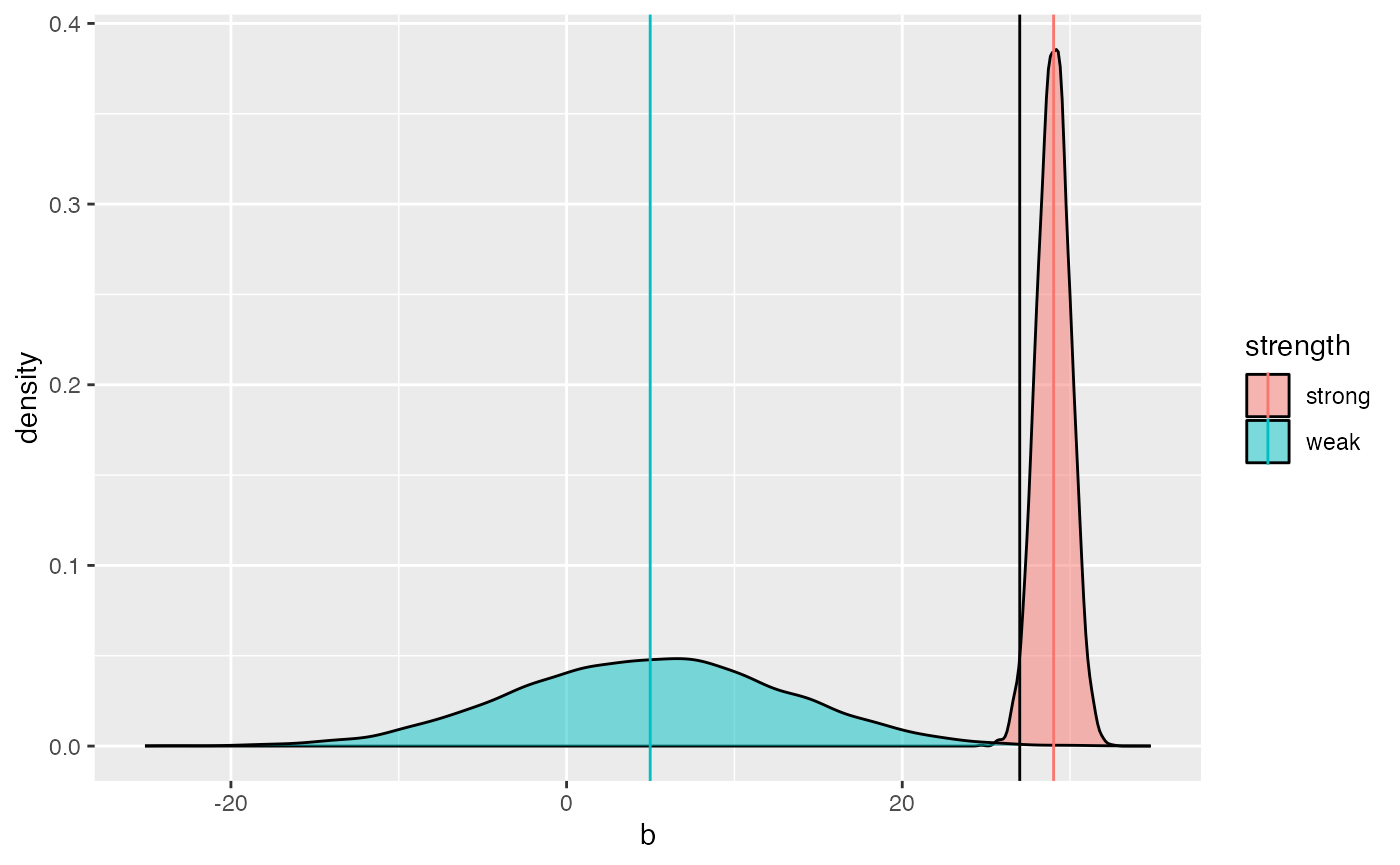
Winner’s curse schematic

library(dplyr)
library(ggplot2)
a <- bind_rows(
    tibble(b=rnorm(10000, 5, sd=8), strength="weak"),
    tibble(b=rnorm(10000, 29, sd=1), strength="strong")
)
ggplot(a, aes(x=b)) +
geom_density(aes(fill=strength), alpha=0.5) +
geom_vline(xintercept=27) +
geom_vline(data=group_by(a, strength) %>% summarise(m=mean(b)), aes(xintercept=m, colour=strength))