library(simulateGP)
library(MASS)
library(tidyverse)
#> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#> ✔ dplyr 1.1.4 ✔ readr 2.1.4
#> ✔ forcats 1.0.0 ✔ stringr 1.5.1
#> ✔ ggplot2 3.4.2 ✔ tibble 3.2.1
#> ✔ lubridate 1.9.2 ✔ tidyr 1.3.0
#> ✔ purrr 1.0.2
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ✖ dplyr::select() masks MASS::select()
#> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(ggplot2)Sample overlap
\[ \begin{bmatrix} \hat{\beta}_1\\ \hat{\beta}_2 \end{bmatrix} = MVN\left ( \begin{bmatrix} \beta_1\\ \beta_2 \end{bmatrix}, \boldsymbol{S} \right ) \]
$$ =
\[\begin{bmatrix} N_1 & \rho_{1,2}\frac{N_O}{\sqrt{N_1 N_2}}\\ \rho_{1,2}\frac{N_O}{\sqrt{N_1 N_2}} & N_2 \end{bmatrix}\]$$
betas <- function(b1, b2, se1, se2, n1, n2, pcor, n_overlap, Nrep=1)
{
mu <- c(b1,b2)
# se1 and se2 are computed as per your formula
ses <- matrix(c(se1,0, 0, se2), 2, 2)
# pcor is the phenotypic correlation between traits, N_0 is the sample overlap, N1 is sample size 1, N2 is sample size 2
r <- pcor * n_overlap / sqrt(n1*n2)
cor = matrix(c(1,r, r, 1), 2, 2)
cov <- ses %*% cor %*% ses
sample <- mvrnorm(Nrep, mu, cov)
sample
}
maf <- 0.4
vy <- 1
n1 <- 10000
n2 <- 10000
b1 <- 0.1
bxy <- 0
b2 <- b1 * bxy
se1 <- expected_se(b1, maf, n1, 1)
(b1 / se1)^2
#> [1] 48.23151
se2 <- expected_se(b2, maf, n2, 1)
betas(b1, b2, se1, se2, 1000, 1000, 0.5, n_overlap=1000, 10000) %>% colMeans %>% {.[2]/.[1]}
#> [1] 0.003083205
betas(b1, b2, se1, se2, 1000, 1000, 0.5, n_overlap=0, 10000) %>% colMeans %>% {.[2]/.[1]}
#> [1] -0.0005634219
betas(b1, b2, se1, se2, 1000, 1000, 0.5, n_overlap=1000, 10000) %>% cor
#> [,1] [,2]
#> [1,] 1.0000000 0.5204661
#> [2,] 0.5204661 1.0000000
betas(b1, b2, se1, se2, 1000, 1000, 0.5, n_overlap=0, 10000) %>% cor
#> [,1] [,2]
#> [1,] 1.000000000 -0.007276515
#> [2,] -0.007276515 1.000000000
# rsq = F / (F + n -1)
# rsq F + rsq(n-1) = F
# rsq F - F = -rsq(n-1)
# F (rsq - 1) = - rsq(n - 1)
# F = (rsq - rsq n) / rsq - 1
# rsq = 20 / (20 + 1000 - 1)
nrep=2000
nsnp=100
n1 <- 1000
n2 <- 1000
maf <- 0.4
pcor <- 0.6
a <- generate_gwas_params(tibble(snp=1:nsnp, af=maf), 1, S=5)
a <- expand.grid(b1=a$beta, overlap=c(0, 0.5, 1), bxy=c(0, 0.3)) %>% as_tibble
a$se1 <- expected_se(a$b1, maf, n1, 1)
a$fval <- (a$b1/a$se1)^2
hist(a$fval)
a$b2 <- a$b1 * a$bxy
a$se2 <- expected_se(a$b2, maf, n2, 1)
l <- list()
for(i in 1:nrow(a))
{
r <- betas(a$b1[i], a$b2[i], a$se1[i], a$se2[i], n1, n2, pcor, a$overlap[i] * n1, nrep)
d <- a[i,] %>% slice(rep(row_number(), nrep))
d$bx <- r[,1]
d$by <- r[,2]
l[[i]] <- d
}
dat <- bind_rows(l)
dat$wr <- dat$by/dat$bx
ggplot(subset(dat, wr < 3 & wr > -3), aes(x=fval, y=by/bx)) +
# geom_point(size=0.1, aes(colour=as.factor(overlap))) +
geom_smooth(aes(colour=as.factor(overlap))) +
facet_grid(. ~ bxy) +
scale_colour_brewer(type="qual")
#> `geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'
nsim <- 500
dat1 <- tibble(rsq1=runif(nsim, 0.001, 0.01), overlap=1)
dat2 <- tibble(rsq1=dat1$rsq1, overlap=0)
dat3 <- tibble(rsq1=dat1$rsq1, overlap=0.5)
n1 <- 1000
n2 <- 1000
g1 <- make_geno(n1, 1, 0.4)
g2 <- make_geno(n2, 1, 0.4)
u1 <- rnorm(n1)
u2 <- rnorm(n2)
mid <- round(n2/2)
for(i in 1:nrow(dat1))
{
b <- choose_effects(1, dat1$rsq1[i])
x1 <- make_phen(c(b, sqrt(0.5)), cbind(g1, u1))
x2 <- make_phen(c(b, sqrt(0.5)), cbind(g2, u2))
y1 <- make_phen(c(0.1, -sqrt(0.5)), cbind(x1, u1))
y2 <- make_phen(c(0.1, -sqrt(0.5)), cbind(x2, u2))
e1 <- get_effs(x1, y1, g1)
ex1 <- fast_assoc(x1, g1)
ey1 <- fast_assoc(y1, g1)
ey2 <- fast_assoc(y2, g2)
ey3 <- fast_assoc(c(y1[1:mid], y2[(mid+1):n2]), c(g1[1:mid], g2[(mid+1):n2]))
dat1$fval[i] <- ex1$fval
dat2$fval[i] <- ex1$fval
dat3$fval[i] <- ex1$fval
dat1$bx[i] <- ex1$bhat
dat1$by[i] <- ey1$bhat
dat2$bx[i] <- ex1$bhat
dat2$by[i] <- ey2$bhat
dat3$bx[i] <- ex1$bhat
dat3$by[i] <- ey3$bhat
}
#> Warning: Unknown or uninitialised column: `fval`.
#> Unknown or uninitialised column: `fval`.
#> Unknown or uninitialised column: `fval`.
#> Warning: Unknown or uninitialised column: `bx`.
#> Warning: Unknown or uninitialised column: `by`.
#> Warning: Unknown or uninitialised column: `bx`.
#> Warning: Unknown or uninitialised column: `by`.
#> Warning: Unknown or uninitialised column: `bx`.
#> Warning: Unknown or uninitialised column: `by`.
dat <- bind_rows(dat1, dat2, dat3)
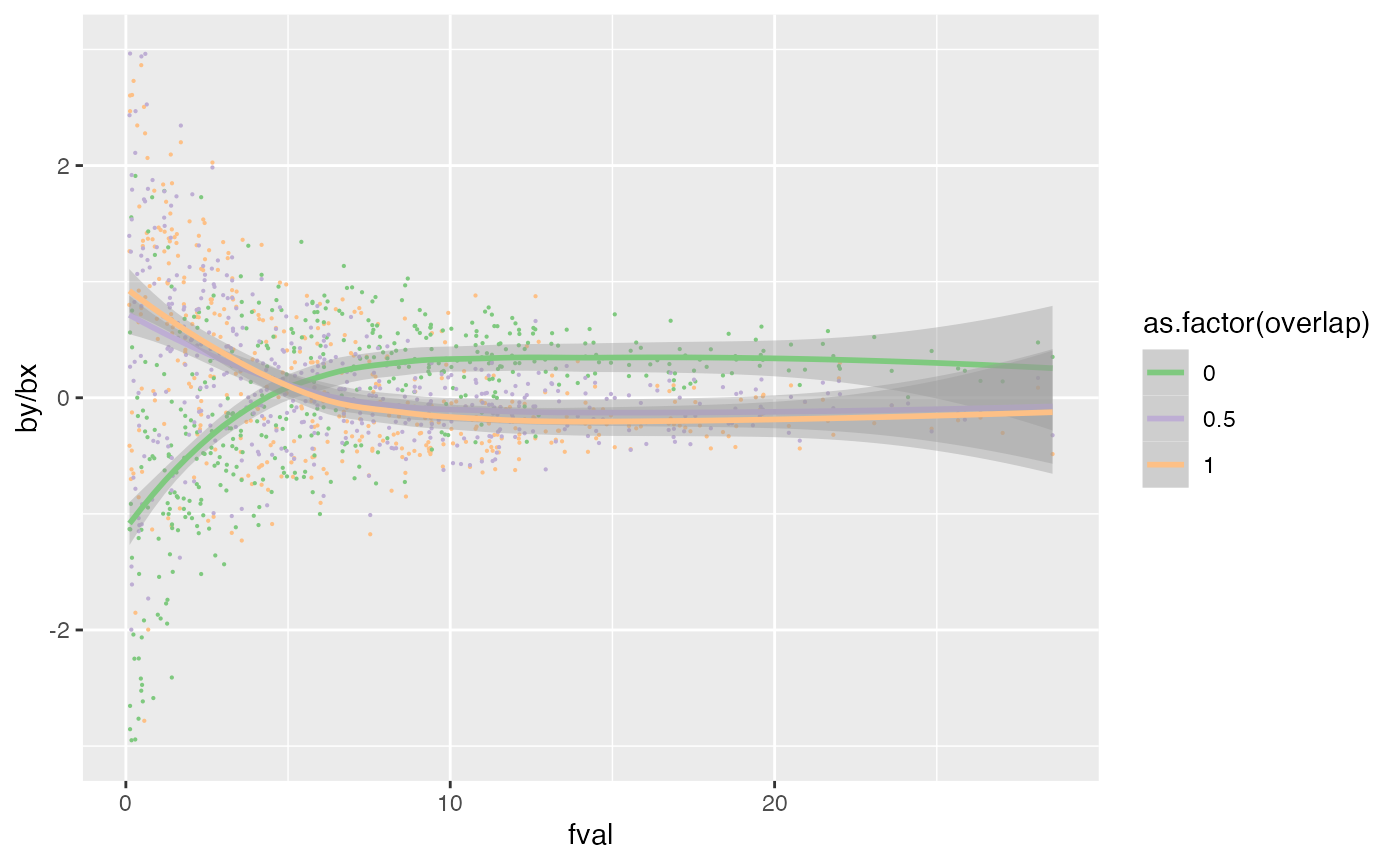
ggplot(dat, aes(x=fval, y=by/bx)) +
geom_point(size=0.1, aes(colour=as.factor(overlap))) +
geom_smooth(aes(colour=as.factor(overlap))) +
xlim(c(0.1, max(dat$fval))) +
ylim(c(-3, 3)) +
scale_colour_brewer(type="qual")
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
#> Warning: Removed 106 rows containing non-finite values
#> (`stat_smooth()`).
#> Warning: Removed 106 rows containing missing values (`geom_point()`).