Residuals for PRS to overcome issue of non-independence

Author

Gibran Hemani

Published

October 10, 2025

Background

If \(Y\) includes related samples, why is it beneficial to adjust for PRS, or to take residuals from the LMM, in order to perform regression without the issue of non-independence?

Data generating model:

\[ Y = \sigma^2_g K + \sigma^2_e I \]

where \(K\) is the kinship matrix and \(I\) is the identity matrix.

The PRS is an estimate of \(\sigma^2_g K\), which means the residual of \(Y\) will reduce to the uncorrelated term \(\sigma^2_e I\). However it’s not clear how well the PRS method will work if it’s an imperfect measure of \(\sigma^2_g K\), and it also is a question as to whether correcting for the complete or incomplete PRS will help with vQTL estimates.

  1. Create y from lots of gs
  2. duplicate some values of y
  3. regress x on y
  4. predict y from gs and adjust for prediction
  5. regression x on y resid
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(ggplot2)

group_size <- 20
ngroup <- 50
n <- group_size * ngroup
p <- 100
g <- matrix(rbinom(group_size * p, 2, 0.5), group_size, p)
betas <- rnorm(p)

prs <- rep(scale(g %*% betas), each=ngroup)
e <- rnorm(n)
y <- (prs + e) %>% scale %>% drop

Now generate estimates of the PRS.

  • Betas are imperfectly estimates
  • Only some Betas are included
betahat <- rnorm(p, betas)
prshat1 <- rep(scale(g %*% betahat), each=ngroup)
prshat2 <- rep(scale(g[,1:(p/2)] %*% betas[1:(p/2)]), each=ngroup)
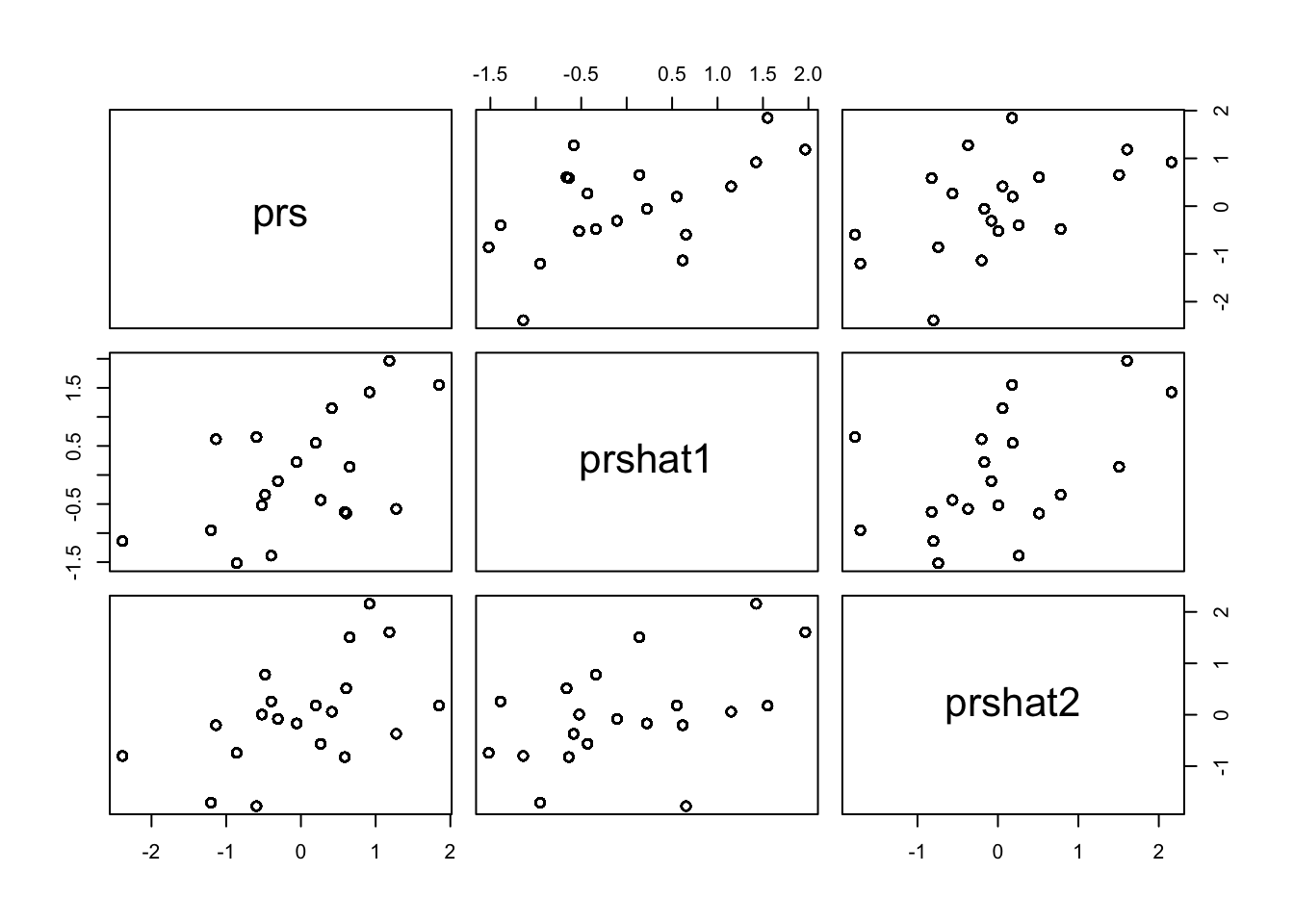
pairs(cbind(prs, prshat1, prshat2))

Generate residuals

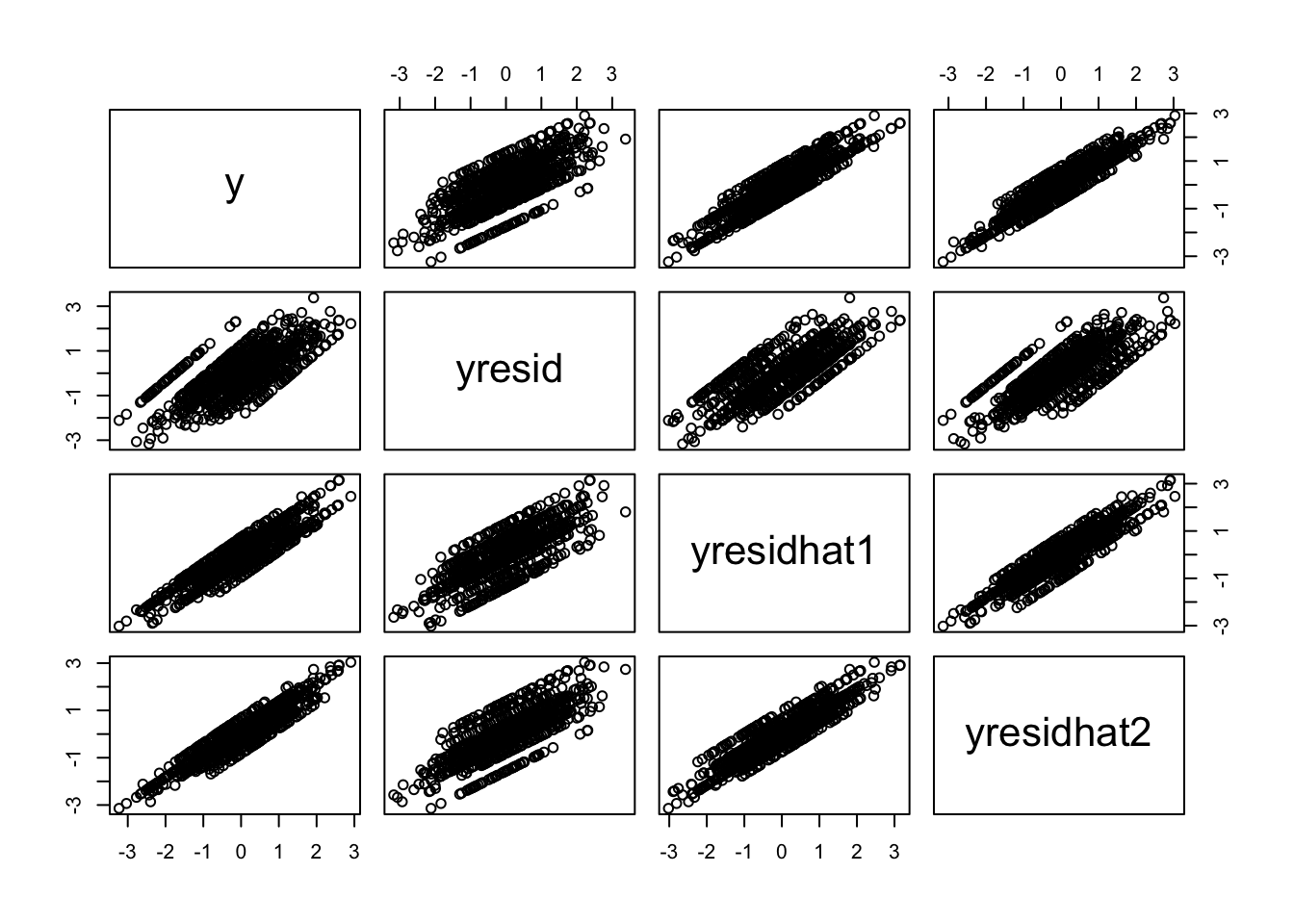
yresid <- residuals(lm(y ~ prs)) %>% scale %>% drop
yresidhat1 <- residuals(lm(y ~ prshat1)) %>% scale %>% drop
yresidhat2 <- residuals(lm(y ~ prshat2)) %>% scale %>% drop
pairs(cbind(y, yresid, yresidhat1, yresidhat2))

Function for vQTL estimation

drm <- function(g, y) {
  y.i <- tapply(y, g, median, na.rm=T)  
  z.ij <- abs(y - y.i[g+1])
  summary(lm(z.ij ~ g))$coef %>%
    as_tibble() %>%
    slice(2) %>%
    mutate(method="drm")
}

add <- function(g, y) {
    summary(lm(y ~ g))$coef %>%
    as_tibble() %>%
    slice(2) %>%
    mutate(method="add")
}

Run simulations

  • Null SNP
  • Strong relatedness
  • Y is adjusted for different levels of PRS
  • Additive (add) and vQTL models (drm)
  • 1000 replicates
params <- expand.grid(
    y_options = c("y", "yresid", "yresidhat1", "yresidhat2"),
    method_options = c("drm", "add"),
    stringsAsFactors=FALSE
)

sims <- lapply(1:1000, \(i) {
    SNP <- rep(rbinom(group_size, 2, 0.5), each = ngroup)
    lapply(1:nrow(params), \(j) {
        m <- get(params$method_options[j])
        yo <- get(params$y_options[j])
        m(SNP, yo) %>% mutate(what = params$y_options[j])
    }) %>% bind_rows()

}) %>% bind_rows()
names(sims) <- c("b", "se", "tval", "pval", "method", "what")
sims
# A tibble: 7,984 × 6
          b     se   tval     pval method what      
      <dbl>  <dbl>  <dbl>    <dbl> <chr>  <chr>     
 1  0.0695  0.0216  3.22  1.31e- 3 drm    y         
 2  0.0112  0.0222  0.503 6.15e- 1 drm    yresid    
 3  0.00680 0.0214  0.318 7.51e- 1 drm    yresidhat1
 4  0.0108  0.0212  0.511 6.10e- 1 drm    yresidhat2
 5 -0.0627  0.0365 -1.72  8.63e- 2 add    y         
 6 -0.0393  0.0366 -1.07  2.83e- 1 add    yresid    
 7 -0.224   0.0359 -6.23  6.70e-10 add    yresidhat1
 8 -0.281   0.0355 -7.91  6.70e-15 add    yresidhat2
 9  0.162   0.0308  5.26  1.72e- 7 drm    y         
10  0.0141  0.0327  0.432 6.66e- 1 drm    yresid    
# ℹ 7,974 more rows

Mean absolute values from the simulations

sims %>% group_by(method, what) %>% summarise(b=mean(abs(b)), se=mean(se), pval=mean(pval), tval=mean(abs(tval)))
`summarise()` has grouped output by 'method'. You can override using the
`.groups` argument.
# A tibble: 8 × 6
# Groups:   method [2]
  method what            b     se  pval  tval
  <chr>  <chr>       <dbl>  <dbl> <dbl> <dbl>
1 add    y          0.204  0.0460 0.116 4.53 
2 add    yresid     0.0485 0.0467 0.415 1.04 
3 add    yresidhat1 0.183  0.0462 0.129 4.03 
4 add    yresidhat2 0.194  0.0461 0.125 4.28 
5 drm    y          0.0778 0.0273 0.174 2.88 
6 drm    yresid     0.0179 0.0283 0.568 0.630
7 drm    yresidhat1 0.0597 0.0271 0.220 2.21 
8 drm    yresidhat2 0.0714 0.0274 0.186 2.62

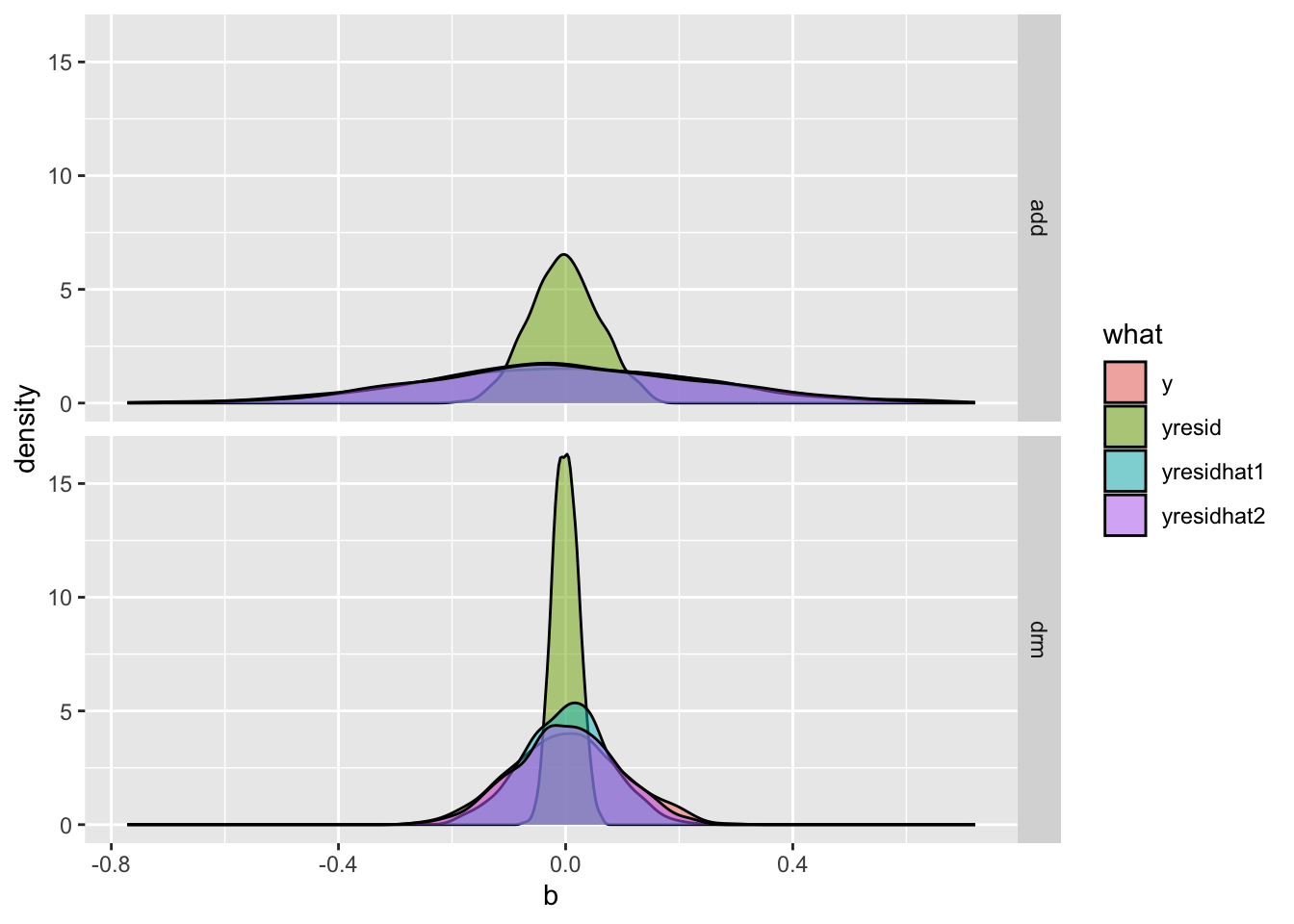
Look at difference in betas

ggplot(sims, aes(x=b)) +
geom_density(aes(fill=what), alpha=0.5) +
facet_grid(method ~ .)

Summary

  • Full adjustment for PRS will remove type 1 error for both vQTLs and additive effects
  • The standard error is not affected by the adjustment
  • The betas are attenuated when PRS is more effectively captured
sessionInfo()
R version 4.5.1 (2025-06-13)
Platform: aarch64-apple-darwin20
Running under: macOS Sonoma 14.6.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ggplot2_3.5.2 dplyr_1.1.4  

loaded via a namespace (and not attached):
 [1] vctrs_0.6.5        cli_3.6.5          knitr_1.50         rlang_1.1.6       
 [5] xfun_0.52          generics_0.1.4     jsonlite_2.0.0     labeling_0.4.3    
 [9] glue_1.8.0         htmltools_0.5.8.1  scales_1.4.0       rmarkdown_2.29    
[13] grid_4.5.1         evaluate_1.0.4     tibble_3.3.0       fastmap_1.2.0     
[17] yaml_2.3.10        lifecycle_1.0.4    compiler_4.5.1     RColorBrewer_1.1-3
[21] htmlwidgets_1.6.4  pkgconfig_2.0.3    farver_2.1.2       digest_0.6.37     
[25] R6_2.6.1           utf8_1.2.6         tidyselect_1.2.1   pillar_1.11.0     
[29] magrittr_2.0.3     withr_3.0.2        tools_4.5.1        gtable_0.3.6