MVMR interpretation with differential power

Author

Gibran Hemani

Published

August 14, 2025

Background

Suppose this is the model:

G1 -> childhood BMI
         | 
         V
G2 -> adulthood BMI -> BC

If the childhood BMI GWAS and the adulthood GWAS are different sample sizes, how does this influence the MVMR performance?

Simulations

library(simulateGP)
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(furrr)
Loading required package: future
library(ggplot2)

do_mvmr <- function(ss1, ss2, ssout) {
    snplist <- c(
        subset(ss1, pval < 5e-8)$snp,
        subset(ss2, pval < 5e-8)$snp
    ) %>% unique
    b1 <- subset(ss1, snp %in% snplist)$bhat
    b2 <- subset(ss2, snp %in% snplist)$bhat
    bout <- subset(ssout, snp %in% snplist)$bhat
    seout <- subset(ssout, snp %in% snplist)$se
    mod <- summary(lm(bout ~ 0 + b1 + b2, weight=1/seout^2))$coef %>% as_tibble()
    names(mod) <- c("b", "se", "tval", "pval")
    mod <- mutate(mod, trait=c("1", "2"), ninst = c(sum(ss1$pval < 5e-8), sum(ss2$pval < 5e-8)))
    return(mod)
}

generate_data <- function(nsnp, h2_1, h2_2, Pi_1, Pi_2, b_12, nid1, nid2, nid3, b_1o, b_2o, rep=NULL, gxe=NULL) {
    map <- arbitrary_map(runif(nsnp, 0.01, 0.99))

    params1 <- generate_gwas_params(map=map, h2=h2_1, S=-0.1, Pi=Pi_1)
    params2 <- generate_gwas_params(map=map, h2=h2_2, S=-0.1, Pi=Pi_2)
    params2$beta <- params2$beta + params1$beta * b_12

    ss1 <- generate_gwas_ss(params1, nid=nid1)
    ss2 <- generate_gwas_ss(params2, nid=nid2)

    params3 <- params2
    params3$beta <- params1$beta * b_1o + params2$beta * b_2o
    ssout <- generate_gwas_ss(params3, nid=300000)
    return(list(ss1, ss2, ssout))
}

Example

dat <- generate_data(
    nsnp = 1000000,
    h2_1 = 0.3,
    h2_2 = 0.3,
    Pi_1 = 0.02,
    Pi_2 = 0.02,
    b_12 = 0.8,
    nid1 = 220000,
    nid2 = 220000,
    nid3 = 300000,
    b_1o = 0,
    b_2o = -0.5
)

str(dat)
List of 3
 $ : tibble [1,000,000 × 11] (S3: tbl_df/tbl/data.frame)
  ..$ snp : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ chr : num [1:1000000] 99 99 99 99 99 99 99 99 99 99 ...
  ..$ pos : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ ea  : chr [1:1000000] "1" "1" "1" "1" ...
  ..$ oa  : chr [1:1000000] "2" "2" "2" "2" ...
  ..$ af  : num [1:1000000] 0.325 0.329 0.491 0.247 0.419 ...
  ..$ se  : num [1:1000000] 0.00322 0.00321 0.00302 0.00349 0.00306 ...
  ..$ bhat: num [1:1000000] 1.04e-03 4.80e-05 1.01e-03 6.61e-04 6.47e-05 ...
  ..$ fval: num [1:1000000] 0.104388 0.000223 0.113153 0.03582 0.000448 ...
  ..$ n   : num [1:1000000] 220000 220000 220000 220000 220000 220000 220000 220000 220000 220000 ...
  ..$ pval: num [1:1000000] 0.747 0.988 0.737 0.85 0.983 ...
 $ : tibble [1,000,000 × 11] (S3: tbl_df/tbl/data.frame)
  ..$ snp : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ chr : num [1:1000000] 99 99 99 99 99 99 99 99 99 99 ...
  ..$ pos : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ ea  : chr [1:1000000] "1" "1" "1" "1" ...
  ..$ oa  : chr [1:1000000] "2" "2" "2" "2" ...
  ..$ af  : num [1:1000000] 0.325 0.329 0.491 0.247 0.419 ...
  ..$ se  : num [1:1000000] 0.00322 0.00321 0.00302 0.00349 0.00306 ...
  ..$ bhat: num [1:1000000] -1.87e-04 -1.81e-04 3.02e-04 2.84e-05 1.54e-03 ...
  ..$ fval: num [1:1000000] 3.37e-03 3.18e-03 1.00e-02 6.62e-05 2.53e-01 ...
  ..$ n   : num [1:1000000] 220000 220000 220000 220000 220000 220000 220000 220000 220000 220000 ...
  ..$ pval: num [1:1000000] 0.954 0.955 0.92 0.994 0.615 ...
 $ : tibble [1,000,000 × 11] (S3: tbl_df/tbl/data.frame)
  ..$ snp : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ chr : num [1:1000000] 99 99 99 99 99 99 99 99 99 99 ...
  ..$ pos : int [1:1000000] 1 2 3 4 5 6 7 8 9 10 ...
  ..$ ea  : chr [1:1000000] "1" "1" "1" "1" ...
  ..$ oa  : chr [1:1000000] "2" "2" "2" "2" ...
  ..$ af  : num [1:1000000] 0.325 0.329 0.491 0.247 0.419 ...
  ..$ se  : num [1:1000000] 0.00276 0.00275 0.00258 0.00299 0.00262 ...
  ..$ bhat: num [1:1000000] 0.00207 0.000835 0.003009 0.001452 -0.003564 ...
  ..$ fval: num [1:1000000] 0.5643 0.0923 1.3579 0.2355 1.8554 ...
  ..$ n   : num [1:1000000] 3e+05 3e+05 3e+05 3e+05 3e+05 3e+05 3e+05 3e+05 3e+05 3e+05 ...
  ..$ pval: num [1:1000000] 0.453 0.761 0.244 0.628 0.173 ...
do_mvmr(dat[[1]], dat[[2]], dat[[3]])
# A tibble: 2 × 6
        b     se   tval      pval trait ninst
    <dbl>  <dbl>  <dbl>     <dbl> <chr> <int>
1 -0.0651 0.0128  -5.07 5.67e-  7 1       230
2 -0.390  0.0110 -35.6  1.16e-136 2       283

Here, the power is the same for the two exposures, and we get an appropriate result of exposure 2 having the causal influence.

Analysis

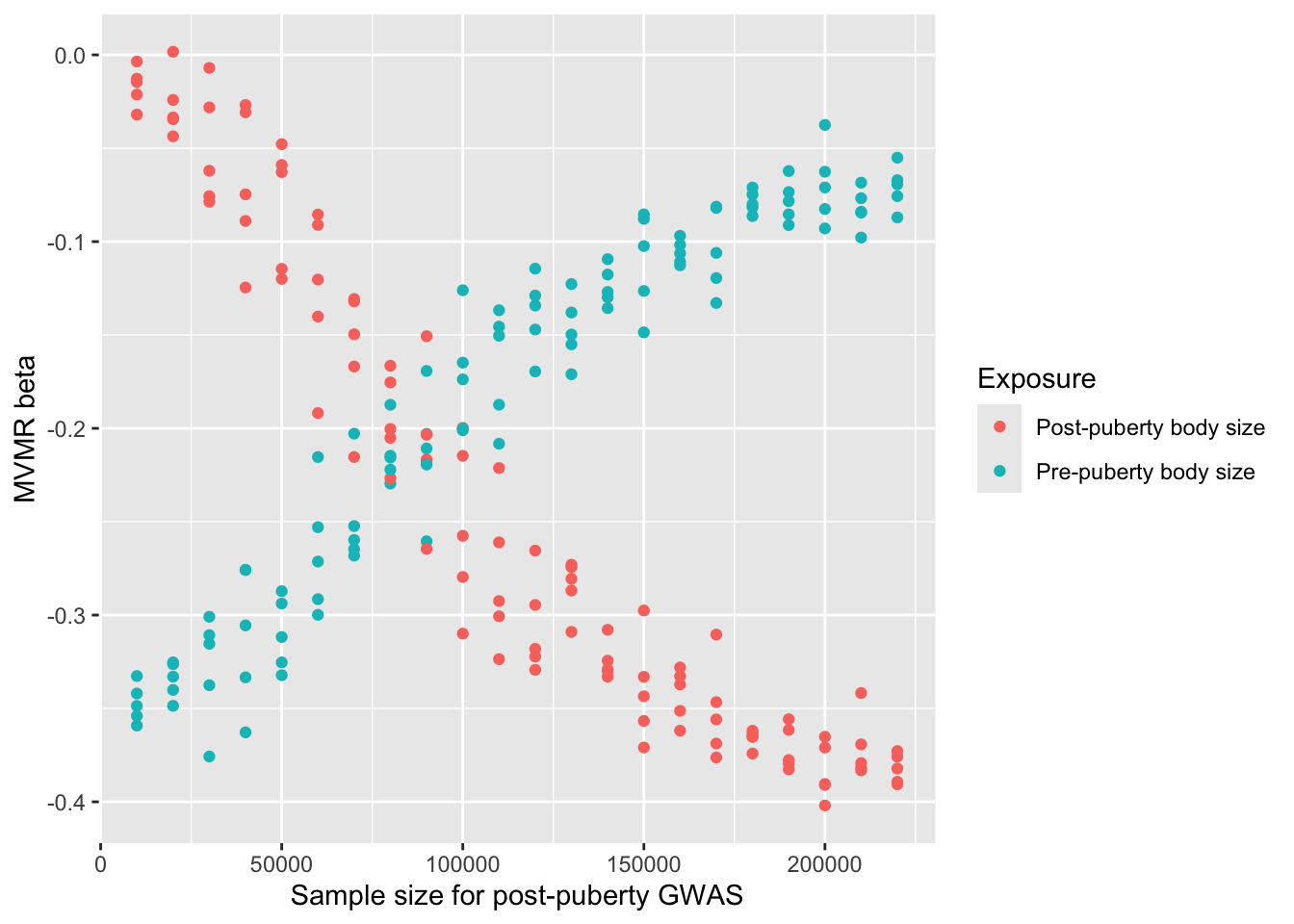
Run simulations with different sample sizes for the exposure 2 (the real causal exposure)

params <- expand.grid(
    nsnp = 1000000,
    h2_1 = 0.3,
    h2_2 = 0.1,
    Pi_1 = 0.02,
    Pi_2 = 0.005,
    b_12 = 0.9,
    gxe = 0,
    nid1 = 220000,
    nid2 = seq(10000, 220000, by=10000),
    nid3 = 300000,
    b_1o = 0,
    b_2o = -0.5,
    rep = 1:5
)

run_sim <- function(...) {
    l <- list(...)
    dat <- do.call(generate_data, l)
    res <- do_mvmr(dat[[1]], dat[[2]], dat[[3]])
    res <- bind_cols(res, as_tibble(l))
}

plan(multicore, workers=6)

res <- future_pmap(params, run_sim, .options=furrr_options(seed=TRUE)) %>% bind_rows()
res %>% mutate(
    trait = case_when(trait == 1 ~ "Pre-puberty body size", trait == 2 ~ "Post-puberty body size")
) %>%
ggplot(aes(x=nid2, y=b, colour=as.factor(trait))) +
geom_point() +
labs(x="Sample size for post-puberty GWAS", y="MVMR beta", colour="Exposure")

Summary

This is probably well known, but when X2 is causal but has low power, X1 will appear to be the causal factor

Empirically we see the below, so this power issue is not the whole story.

childhood (high power)
  |
  v
adolescent (low power) -> BC

- adolescent attenuates when power is low





adolescent (low power) -> BC
  |
  v
adult (high power)

- adult attenuates even though power is high
sessionInfo()
R version 4.5.1 (2025-06-13)
Platform: aarch64-apple-darwin20
Running under: macOS Sonoma 14.6.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ggplot2_3.5.2    furrr_0.3.1      future_1.49.0    dplyr_1.1.4     
[5] simulateGP_0.1.3

loaded via a namespace (and not attached):
 [1] gtable_0.3.6       jsonlite_2.0.0     compiler_4.5.1     tidyselect_1.2.1  
 [5] parallel_4.5.1     globals_0.18.0     scales_1.4.0       yaml_2.3.10       
 [9] fastmap_1.2.0      R6_2.6.1           labeling_0.4.3     generics_0.1.4    
[13] knitr_1.50         htmlwidgets_1.6.4  tibble_3.3.0       pillar_1.11.0     
[17] RColorBrewer_1.1-3 rlang_1.1.6        utf8_1.2.6         xfun_0.52         
[21] cli_3.6.5          withr_3.0.2        magrittr_2.0.3     digest_0.6.37     
[25] grid_4.5.1         lifecycle_1.0.4    vctrs_0.6.5        evaluate_1.0.4    
[29] glue_1.8.0         farver_2.1.2       listenv_0.9.1      codetools_0.2-20  
[33] parallelly_1.44.0  rmarkdown_2.29     purrr_1.1.0        tools_4.5.1       
[37] pkgconfig_2.0.3    htmltools_0.5.8.1