Meta analysis including small samples

Author

Gibran Hemani

Published

September 28, 2024

Background

Does meta analysis with very small samples lead to bias?

  • Simulate a regression
  • Split the data into different size groups and meta analyse the groups
  • Compare the meta-analysis results to the full analysis
  • Does smaller group size lead to bias?
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(ggplot2)
library(tidyr)
ivw <- function(betas, ses) {
  weights <- 1 / ses^2
  beta <- sum(weights * betas) / sum(weights)
  se <- 1 / sqrt(sum(weights))
  return(c(beta, se))
}
fast_assoc <- function(y, x) {
    index <- is.finite(y) & is.finite(x)
    n <- sum(index)
    y <- y[index]
    x <- x[index]
    vx <- var(x)
    bhat <- stats::cov(y, x) / vx
    ahat <- mean(y) - bhat * mean(x)
    # fitted <- ahat + x * bhat
    # residuals <- y - fitted
    # SSR <- sum((residuals - mean(residuals))^2)
    # SSF <- sum((fitted - mean(fitted))^2)

    rsq <- (bhat * vx)^2 / (vx * var(y))
    fval <- rsq * (n-2) / (1-rsq)
    tval <- sqrt(fval)
    se <- abs(bhat / tval)

    # Fval <- (SSF) / (SSR/(n-2))
    # pval <- pf(Fval, 1, n-2, lowe=F)
    # p <- stats::pf(fval, 1, n-2, lower.tail=FALSE)
    return(list(
        ahat=ahat, bhat=bhat, se=se, fval=fval, n=n
    ))
}

sim <- function(n, nbreak, beta, af) {
    g <- rbinom(n, 2, af)
    y <- g * beta + rnorm(n)
    full <- summary(lm(y ~ g))
    breaks <- cut(1:n, breaks=nbreak)
    r <- lapply(levels(breaks), \(l) {
        y <- y[breaks == l]
        g <- g[breaks == l]
        if(length(unique(g)) == 1) return(NULL)
        a <- fast_assoc(y, g)
        tibble(
            beta = a$bhat,
            se = a$se
        )
    }) %>% bind_rows()
    meta <- ivw(r$beta, r$se)
    tibble(
        n=n, nbreak=nbreak, beta=beta, af=af,
        bhat=c(full$coefficients[2, 1], meta[1]),
        se=c(full$coefficients[2, 2], meta[2]),
        what=c("full", "meta")
    )
}
sim(10000, 1000, 0.2, 0.5)
# A tibble: 2 × 7
      n nbreak  beta    af  bhat     se what 
  <dbl>  <dbl> <dbl> <dbl> <dbl>  <dbl> <chr>
1 10000   1000   0.2   0.5 0.243 0.0143 full 
2 10000   1000   0.2   0.5 0.243 0.0134 meta 
param <- expand.grid(
    n = 10000,
    nbreak = c(10, 100, 1000),
    beta = c(0, 0.2),
    af = c(0.1, 0.5),
    nsim = 1:30
)
dim(param)
[1] 360   5
res <- lapply(1:nrow(param), \(i) {
    sim(param$n[i], param$nbreak[i], param$beta[i], param$af[i]) %>% mutate(sim=param$nsim[i])
}) %>% bind_rows()
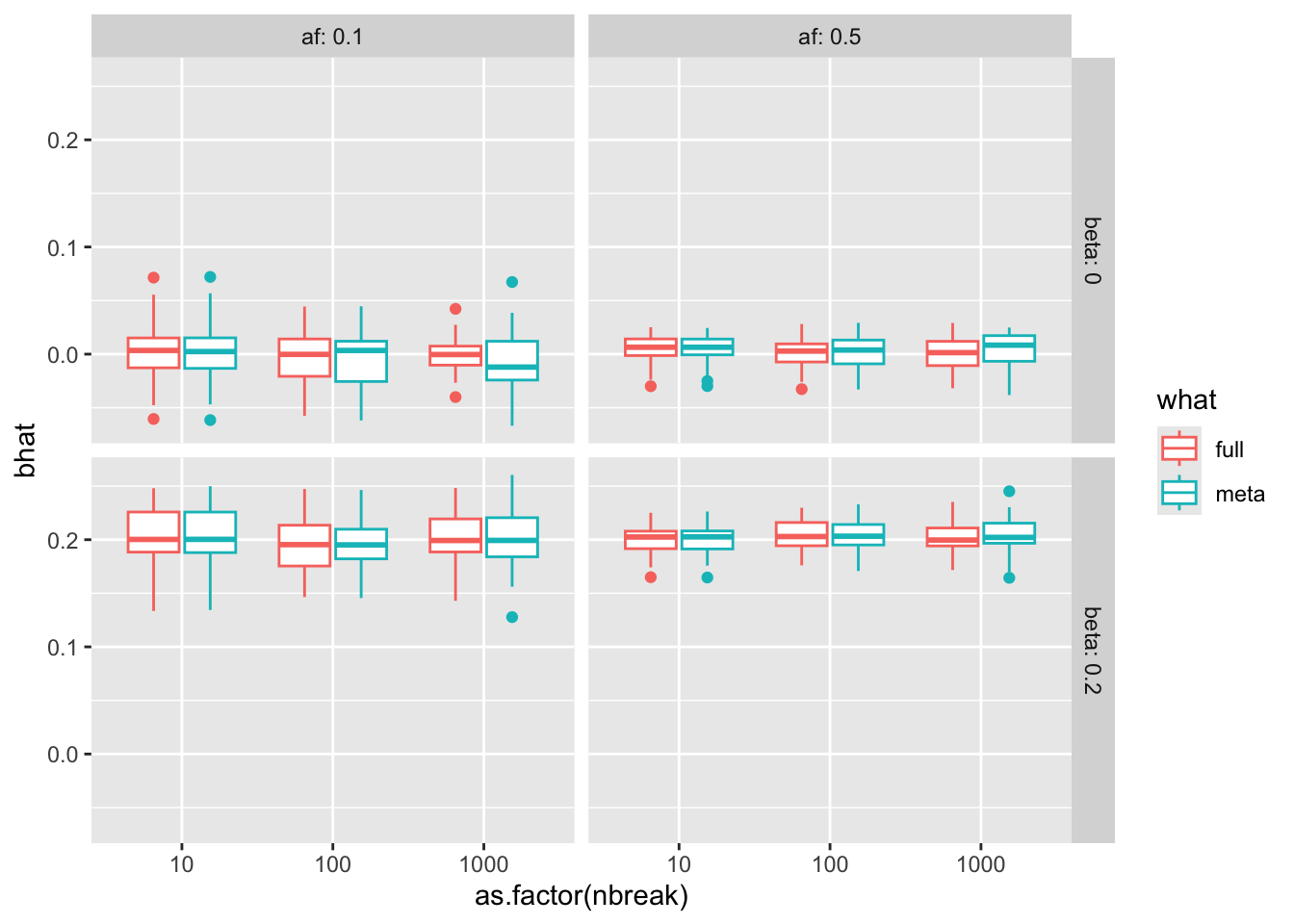
ggplot(res, aes(x=as.factor(nbreak), y=bhat, color=what)) +
    geom_boxplot() +
    facet_grid(beta ~ af, labeller=label_both)

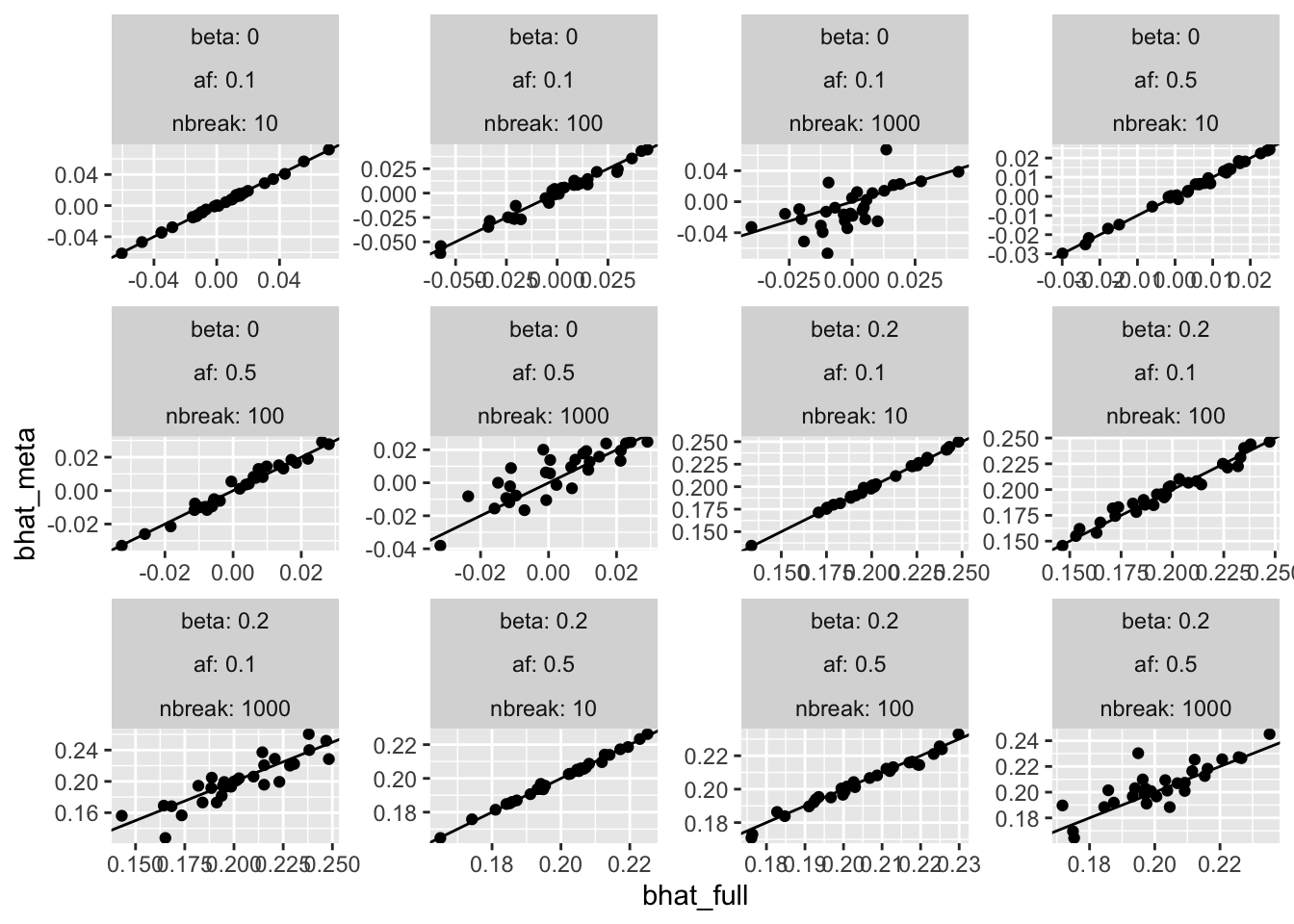
resw <- pivot_wider(res, names_from=what, values_from=c(bhat, se))
ggplot(resw, aes(x=bhat_full, y=bhat_meta)) +
geom_point() +
facet_wrap(~beta + af + nbreak, scale="free", labeller=label_both) +
geom_abline(slope=1, intercept=0)

Try again with just continuous data

sim2 <- function(n, nbreak, beta) {
    g <- rnorm(n)
    y <- g * beta + rnorm(n)
    full <- summary(lm(y ~ g))
    breaks <- cut(1:n, breaks=nbreak)
    r <- lapply(levels(breaks), \(l) {
        y <- y[breaks == l]
        g <- g[breaks == l]
        if(length(unique(g)) == 1) return(NULL)
        a <- fast_assoc(y, g)
        tibble(
            beta = a$bhat,
            se = a$se
        )
    }) %>% bind_rows()
    meta <- ivw(r$beta, r$se)
    tibble(
        n=n, nbreak=nbreak, beta=beta,
        bhat=c(full$coefficients[2, 1], meta[1]),
        se=c(full$coefficients[2, 2], meta[2]),
        what=c("full", "meta")
    )
}
sim2(10000, 1000, 0.2)
# A tibble: 2 × 6
      n nbreak  beta  bhat      se what 
  <dbl>  <dbl> <dbl> <dbl>   <dbl> <chr>
1 10000   1000   0.2 0.196 0.00999 full 
2 10000   1000   0.2 0.192 0.00914 meta 
sim2(10000, 100, 0.2)
# A tibble: 2 × 6
      n nbreak  beta  bhat      se what 
  <dbl>  <dbl> <dbl> <dbl>   <dbl> <chr>
1 10000    100   0.2 0.195 0.00999 full 
2 10000    100   0.2 0.196 0.00995 meta 
sim2(10000, 10, 0.2)
# A tibble: 2 × 6
      n nbreak  beta  bhat     se what 
  <dbl>  <dbl> <dbl> <dbl>  <dbl> <chr>
1 10000     10   0.2 0.202 0.0100 full 
2 10000     10   0.2 0.202 0.0100 meta 
param2 <- expand.grid(
    n = 10000,
    nbreak = c(10, 100, 1000),
    beta = c(0, 0.2),
    nsim = 1:100
)
dim(param2)
[1] 600   4
res2 <- lapply(1:nrow(param2), \(i) {
    sim2(param2$n[i], param2$nbreak[i], param2$beta[i]) %>% mutate(sim=param2$nsim[i])
}) %>% bind_rows()
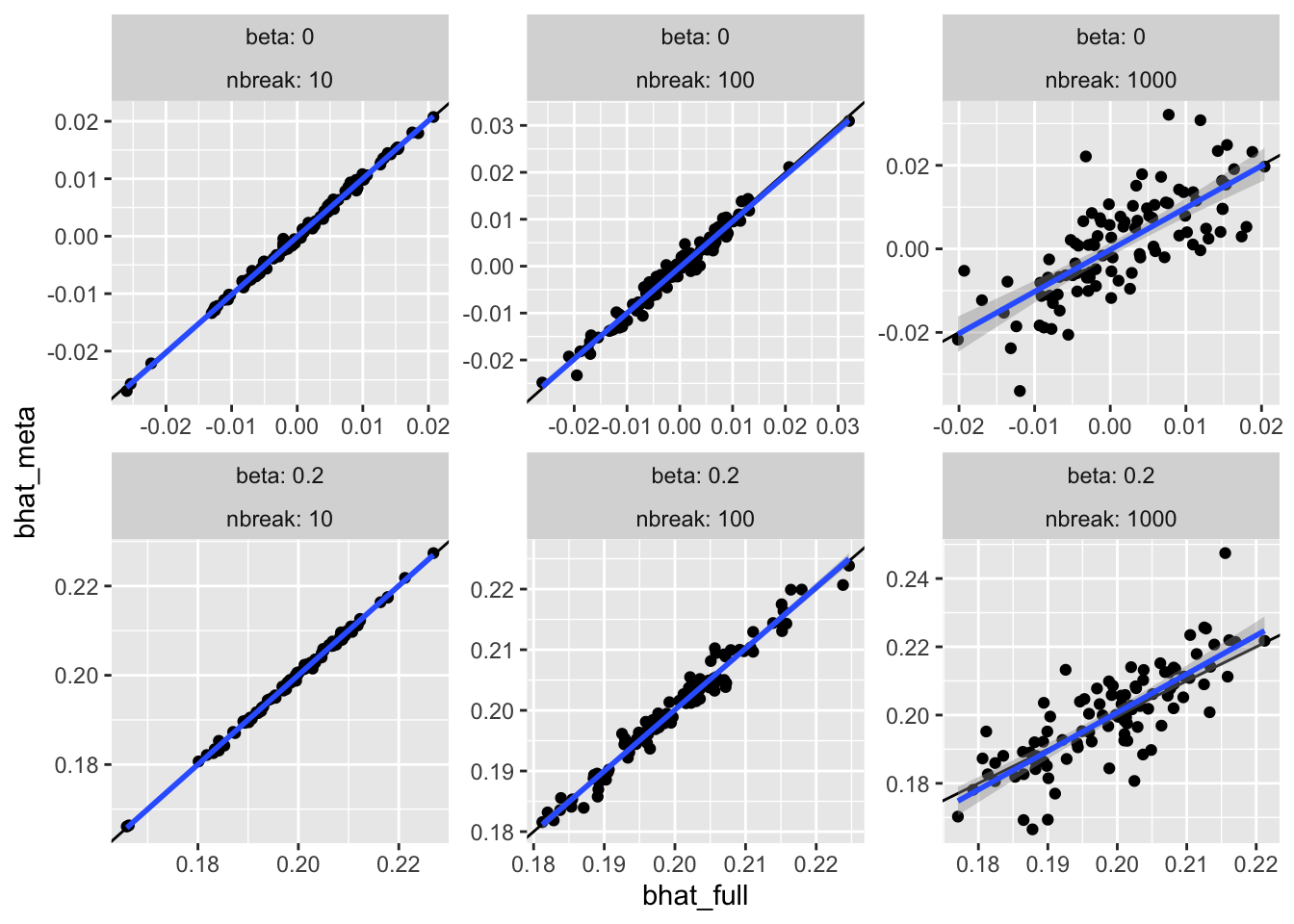
resw <- pivot_wider(res2, names_from=what, values_from=c(bhat, se))
ggplot(resw, aes(x=bhat_full, y=bhat_meta)) +
geom_point() +
facet_wrap(~beta + nbreak, scale="free", labeller=label_both) +
geom_abline(slope=1, intercept=0) +
geom_smooth(method="lm")
`geom_smooth()` using formula = 'y ~ x'

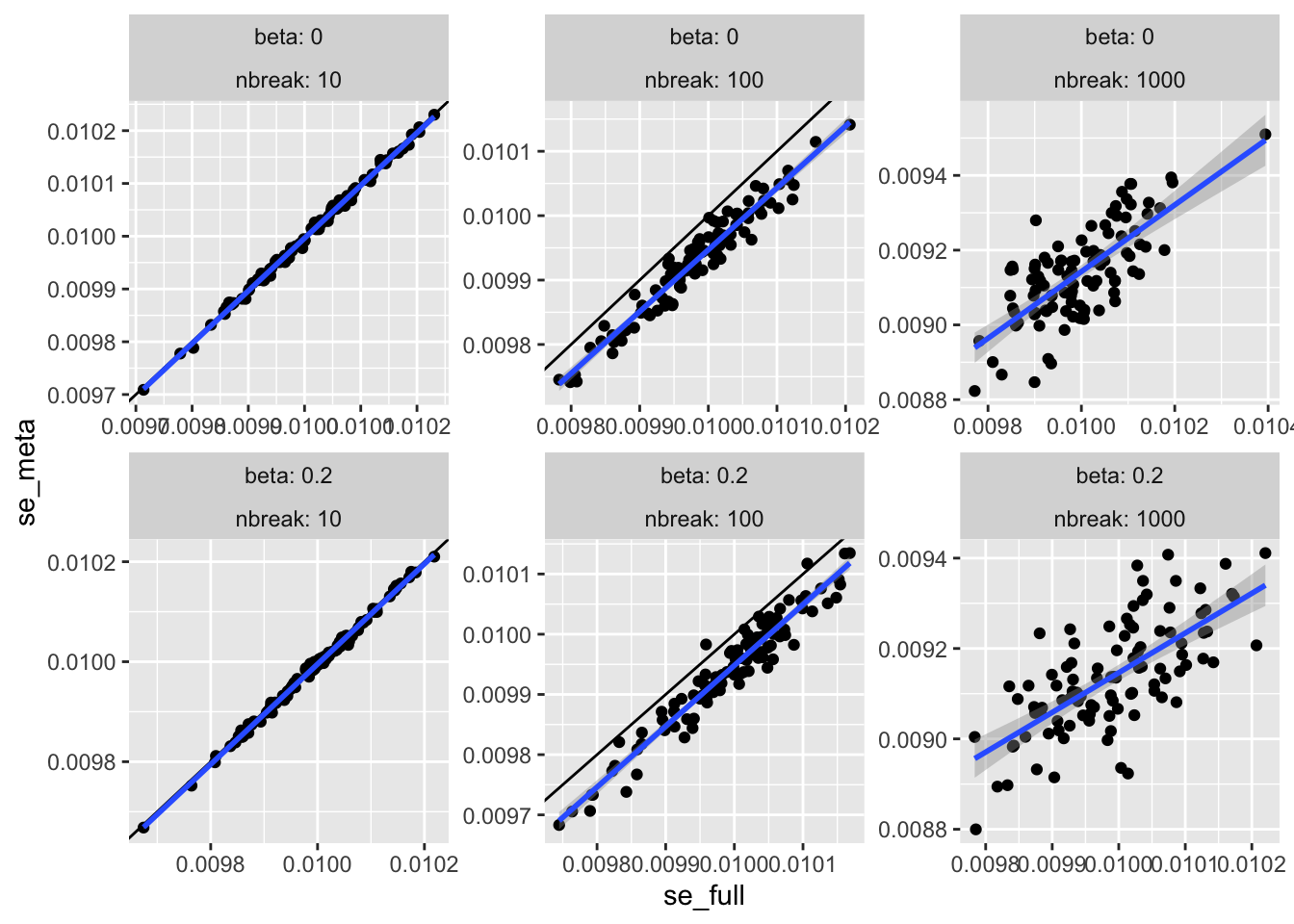
ggplot(resw, aes(x=se_full, y=se_meta)) +
geom_point() +
facet_wrap(~beta + nbreak, scale="free", labeller=label_both) +
geom_abline(slope=1, intercept=0) +
geom_smooth(method="lm")
`geom_smooth()` using formula = 'y ~ x'

res2 %>% 
    mutate(pval = pnorm(abs(bhat)/se, low=F)) %>%
    filter(beta == 0) %>%
    group_by(nbreak, what) %>%
    summarise(power = sum(pval < 0.05)/n(), n=n())
`summarise()` has grouped output by 'nbreak'. You can override using the
`.groups` argument.
# A tibble: 6 × 4
# Groups:   nbreak [3]
  nbreak what  power     n
   <dbl> <chr> <dbl> <int>
1     10 full   0.06   100
2     10 meta   0.06   100
3    100 full   0.1    100
4    100 meta   0.08   100
5   1000 full   0.07   100
6   1000 meta   0.21   100

Simulate one small study

sim3 <- function(n, prop, beta, af) {
    g <- rbinom(n, 2, af)
    y <- g * beta + rnorm(n)

    s1 <- 1:(n*prop)
    s2 <- (1:n)[-s1]
    s3 <- 1:n
    r <- lapply(list(s1, s2, s3), \(s) {
        y <- y[s]
        g <- g[s]
        if(length(unique(g)) == 1) return(NULL)
        a <- fast_assoc(y, g)
        tibble(
            bhat = a$bhat,
            se = a$se,
            ns = length(y)
        )
    }) %>% bind_rows() %>% mutate(what=c("p", "q", "full"))

    meta <- ivw(r$bhat[1:2], r$se[1:2])
    r <- bind_rows(r, tibble(bhat = meta[1], se = meta[2], ns = n, what="meta")) %>%
        mutate(n=n, prop=prop, beta=beta, af=af)
    return(r)
}
sim3(10000, 0.01, 0.2, 0.5)
# A tibble: 4 × 8
   bhat     se    ns what      n  prop  beta    af
  <dbl>  <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 0.153 0.147    100 p     10000  0.01   0.2   0.5
2 0.205 0.0144  9900 q     10000  0.01   0.2   0.5
3 0.204 0.0143 10000 full  10000  0.01   0.2   0.5
4 0.204 0.0143 10000 meta  10000  0.01   0.2   0.5
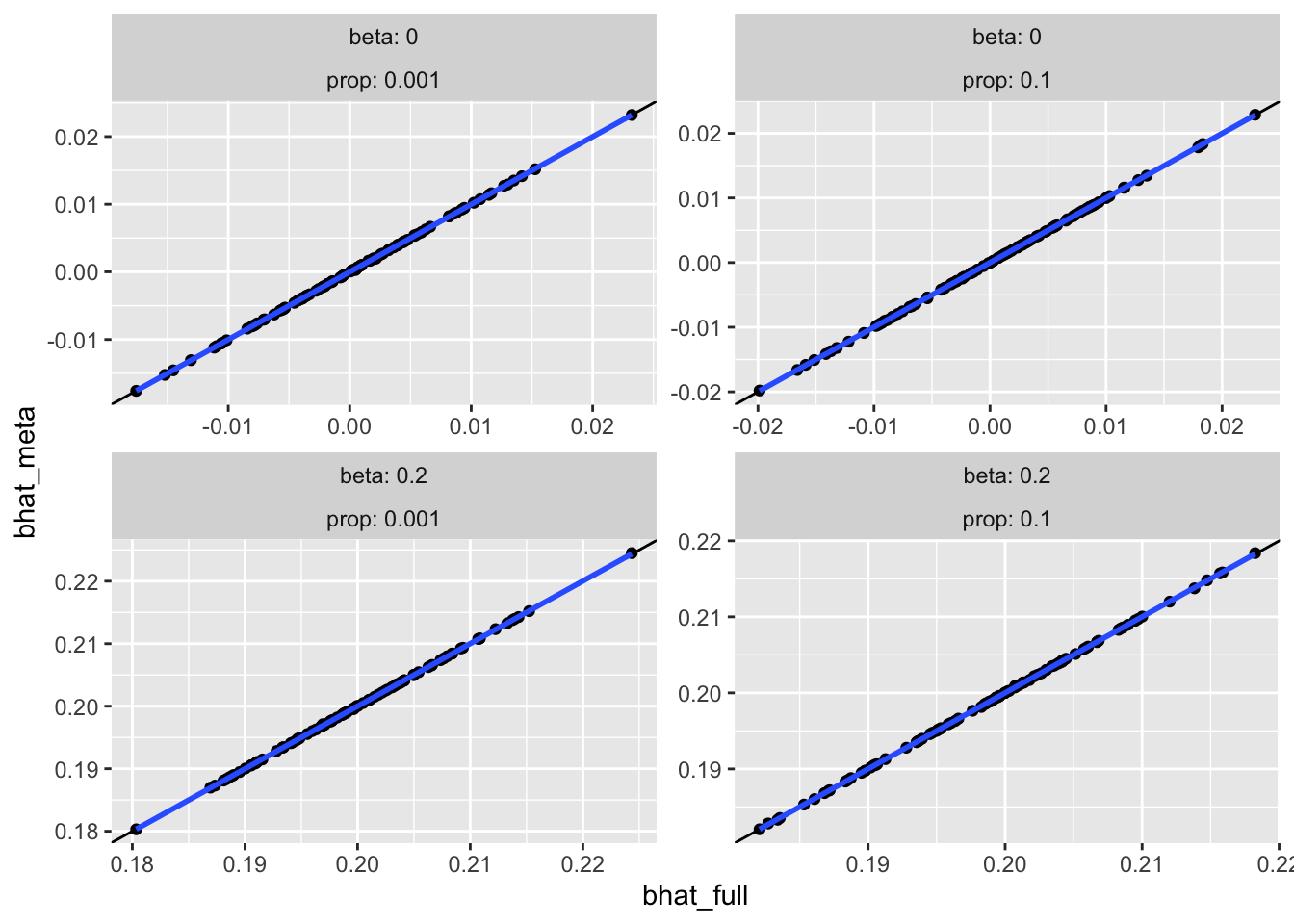
param3 <- expand.grid(
    n = 100000,
    prop = c(0.1, 0.001),
    beta = c(0, 0.2),
    af = c(0.1),
    nsim = 1:100
)
dim(param3)
[1] 400   5
res3 <- lapply(1:nrow(param3), \(i) {
    sim3(param3$n[i], param3$prop[i], param3$beta[i], param3$af[i]) %>% mutate(sim=param3$nsim[i])
}) %>% bind_rows()

resw <- res3 %>% 
    filter(what %in% c("full", "meta")) %>%
    pivot_wider(names_from=what, values_from=c(bhat, se))

ggplot(resw, aes(x=bhat_full, y=bhat_meta)) +
geom_point() +
facet_wrap(~beta + prop, scale="free", labeller=label_both) +
geom_abline(slope=1, intercept=0) +
geom_smooth(method="lm")
`geom_smooth()` using formula = 'y ~ x'

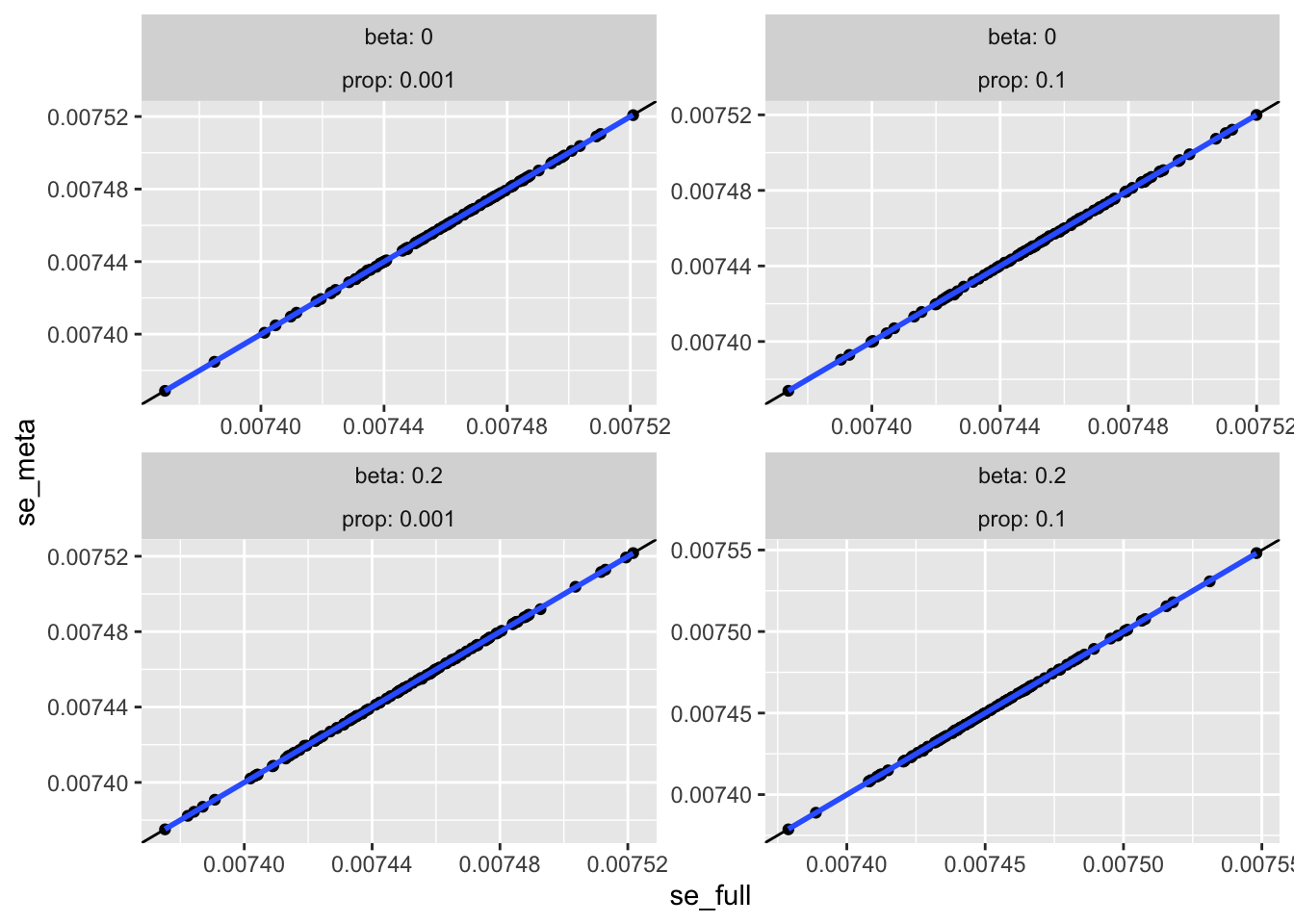
ggplot(resw, aes(x=se_full, y=se_meta)) +
geom_point() +
facet_wrap(~beta + prop, scale="free", labeller=label_both) +
geom_abline(slope=1, intercept=0) +
geom_smooth(method="lm")
`geom_smooth()` using formula = 'y ~ x'

Summary

  • No bias
  • For many small studies, the effects are not identical and become more noisy as the sample size decreases.
  • For many small studies, the standard error is under estimated for the meta analysis as the sample sizes decrease, which leads to slight elevation of type 1 error.
  • For a single small study there is negligible impact on bias or type 1 error.
sessionInfo()
R version 4.4.1 (2024-06-14)
Platform: aarch64-apple-darwin20
Running under: macOS Sonoma 14.6.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] tidyr_1.3.1   ggplot2_3.5.1 dplyr_1.1.4  

loaded via a namespace (and not attached):
 [1] Matrix_1.7-0      gtable_0.3.5      jsonlite_1.8.8    compiler_4.4.1   
 [5] tidyselect_1.2.1  splines_4.4.1     scales_1.3.0      yaml_2.3.8       
 [9] fastmap_1.2.0     lattice_0.22-6    R6_2.5.1          labeling_0.4.3   
[13] generics_0.1.3    knitr_1.47        htmlwidgets_1.6.4 tibble_3.2.1     
[17] munsell_0.5.1     pillar_1.9.0      rlang_1.1.3       utf8_1.2.4       
[21] xfun_0.44         cli_3.6.2         withr_3.0.0       magrittr_2.0.3   
[25] mgcv_1.9-1        digest_0.6.35     grid_4.4.1        lifecycle_1.0.4  
[29] nlme_3.1-164      vctrs_0.6.5       evaluate_0.23     glue_1.7.0       
[33] farver_2.1.2      fansi_1.0.6       colorspace_2.1-0  rmarkdown_2.27   
[37] purrr_1.0.2       tools_4.4.1       pkgconfig_2.0.3   htmltools_0.5.8.1