Expected bias in OLS due to a single confounder

Background

Assuming means are 0, for this system:

\[ \begin{align} x_i &= \beta_{ux} u_i + e_{xi} \\ y_i &= \beta_{uy} u_i + \beta_{xy} x_i + e_{yi} \\ u_i &\sim N(0, \sigma^2_u) \\ e_{xi} &\sim N(0, \sigma^2_{ex}) \\ e_{yi} &\sim N(0, \sigma^2_{ey}) \end{align} \]

What is the expected OLS estimate?

dat <- expand.grid(
    n = 10000,
    bux = c(0.1, 0.2, 1, 2),
    buy = c(0.1, 0.2, 1, 2),
    bxy = c(0, 0.5),
    bgu = c(0.1, 0.5),
    vu = c(1, 0.1, 2),
    vex = c(0.1, 1, 2),
    vey = c(0.1, 1, 2)
)

sim <- function(n, bux, buy, bxy, bgu, vu, vex, vey, ols1=NULL, ols2=NULL, iv1=NULL) {
    g <- rbinom(n, 2, 0.4)
    veu <- vu - var(g) * bgu^2
    if(veu < 0) return(c(NA, NA, NA))
    eu <- rnorm(n, sd=sqrt(veu))
    u <- g * bgu + eu
    ex <- rnorm(n, sd=sqrt(vex))
    ey <- rnorm(n, sd=sqrt(vey))
    x <- u * bux + ex
    y <- u * buy + ey + bxy * x
    
    o <- c(
        lm(y ~ x)$coef[2],
        lm(y ~ u)$coef[2] * lm(x ~ u)$coef[2] + bxy,
        lm(y ~ g)$coef[2] / lm(x ~ g)$coef[2]
    )
    return(o)
}

for(i in 1:nrow(dat)) {
    a <- do.call(sim, dat[i,])
    dat$ols1[i] <- a[1]
    dat$ols2[i] <- a[2] # wrong!
    dat$iv1[i] <- a[3]
}

dat$vx <- with(dat, bux^2 * vu + vex)
dat$ols3 <- with(dat, ((bux * buy + bxy * bux^2) * vu + bxy * vex) / vx)
dat$ols4 <- with(dat, (bux * buy * vu + bxy * vx) / vx)
dat$ols5 <- with(dat, bxy + bux * buy * vu / vx)
dat$rsqux <- with(dat, bux^2 * vu / vx)
dat$ols6 <- with(dat, bxy + buy / bux * rsqux) # final version
dat$iv2 <- with(dat, bxy + buy / bux)

Using the simplified equation where variances aren’t included:

plot(dat$ols1, dat$ols2, xlab="OLS", ylab="bux * buy")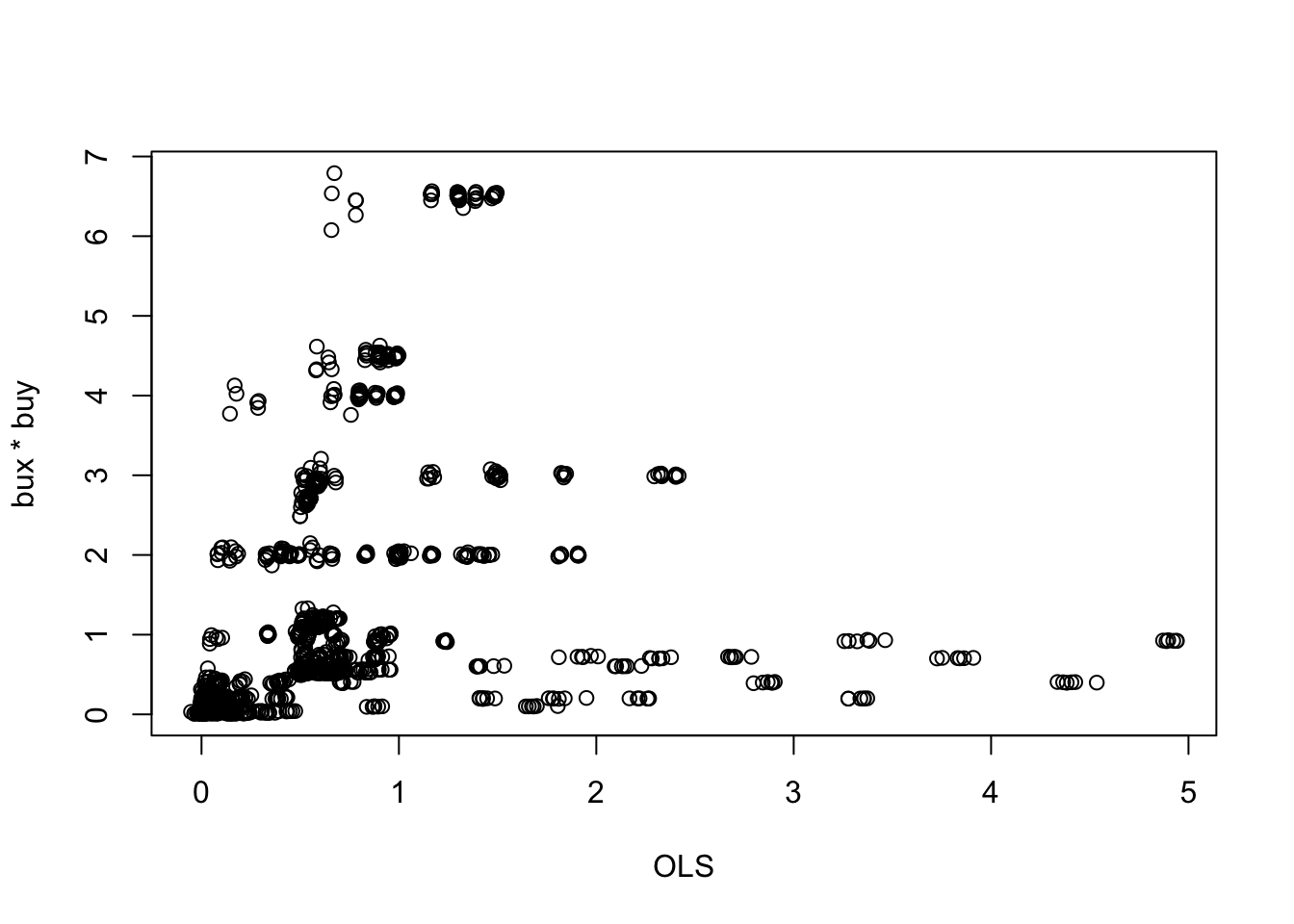

Using the full equation:

plot(dat$ols1, dat$ols5, xlab="OLS", ylab="expected OLS")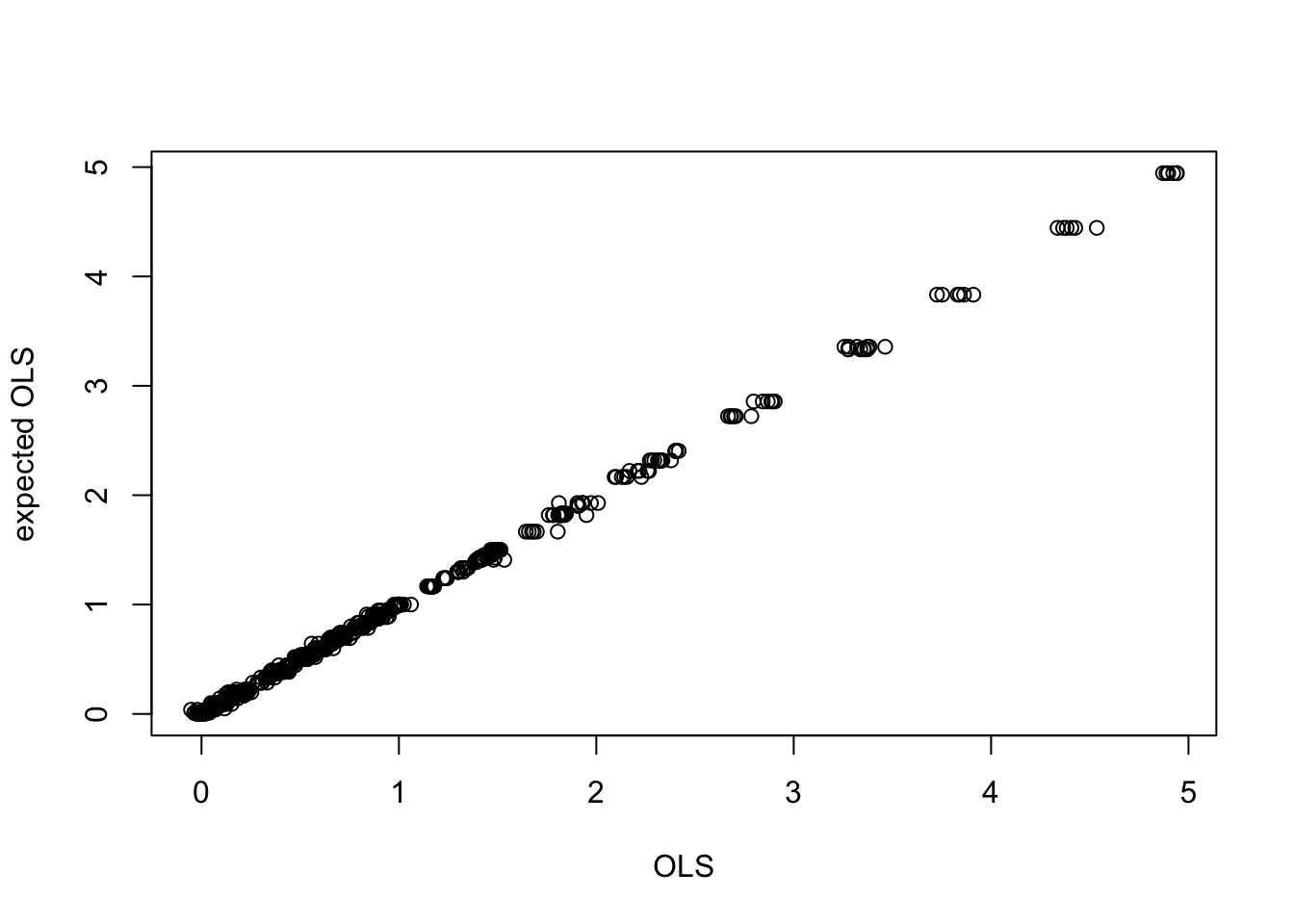

plot(iv2 ~ iv1, data=subset(dat, bux > 0.9), xlab="IV", ylab="expected IV")

Expect that the IV estimate is always more biased than the OLS estimate when instrument arises through U.

plot(iv2 ~ ols1, dat)
abline(0, 1)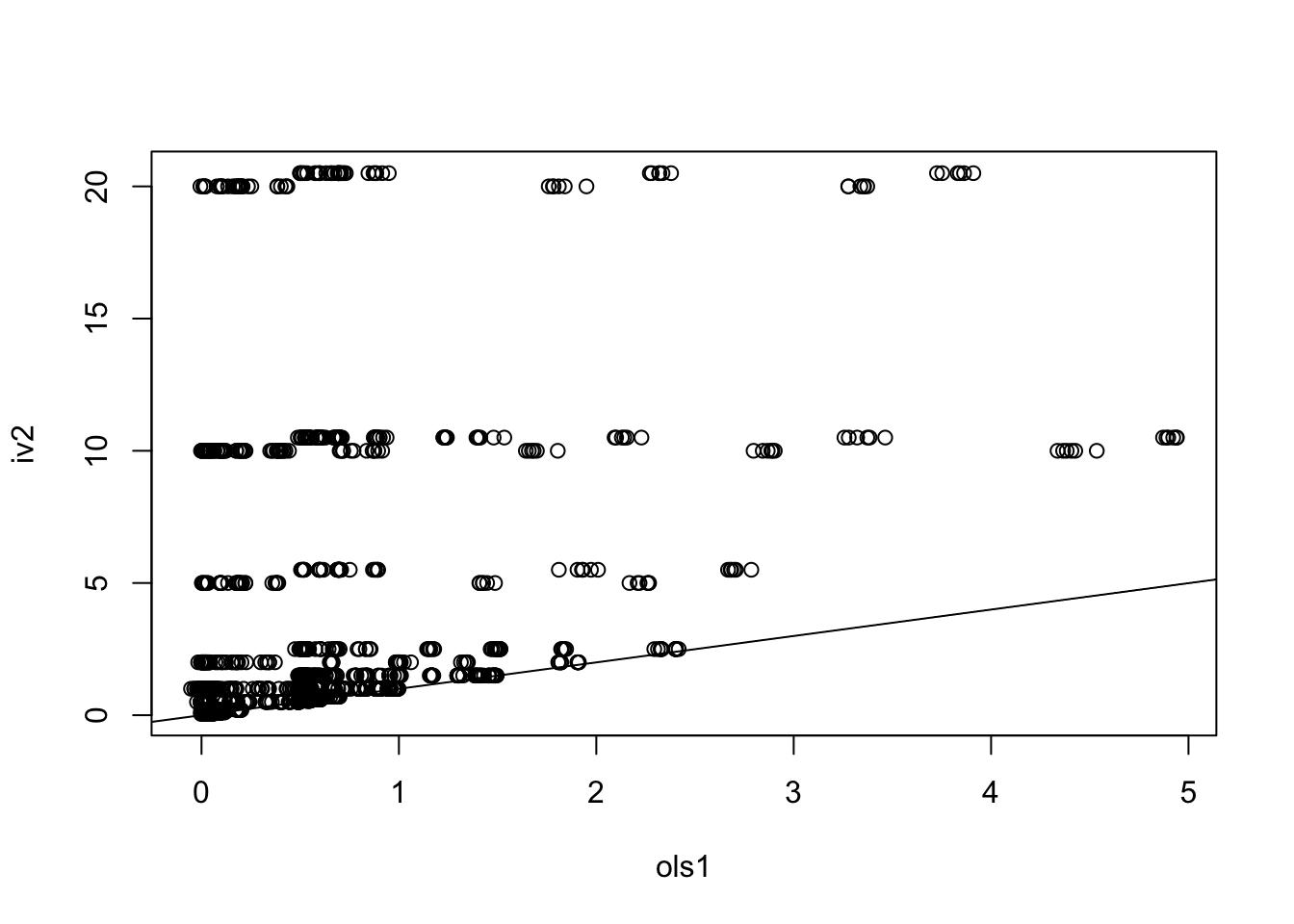

---

sessionInfo()

R version 4.4.1 (2024-06-14)
Platform: aarch64-apple-darwin20
Running under: macOS Ventura 13.6

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/Rome
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] htmlwidgets_1.6.4 compiler_4.4.1    fastmap_1.2.0     cli_3.6.2        
 [5] tools_4.4.1       htmltools_0.5.8.1 yaml_2.3.8        rmarkdown_2.27   
 [9] knitr_1.47        jsonlite_1.8.8    xfun_0.44         digest_0.6.35    
[13] rlang_1.1.3       evaluate_0.23