Time varying MR

Author

Gibran Hemani

Published

January 12, 2024

Background

Work from Panagiota Pagoni looked at time-varying instruments for MR. Idea is to estimate the main and age interaction genetic effects on X, and then perform multivariable MR of main + interaction against outcome.

Simple model below to see what happens…

  1. Simulate n_id individuals with x values for each age ranging from 1:n_age.
  2. There are n_snps and each SNP has a different effect on x before age 15 and after age 15
  3. y is influenced by x at age 12 and x at age 24. The effect of x on y has opposing directions at these two time points.
  4. Estimation
    1. Randomly sample one age point per individual
    2. Estimate either a main effect of each SNP on x to obtain beta_gx, or estimate main + interaction effect of each SNP on x to get beta_gxm and beta_gxi.
    3. Estimate effect of each SNP on y to get beta_gy
    4. Univariable MR of beta_gy ~ beta_gx
    5. Multivariable MR of beta_gy ~ beta_gxm + beta_gxi
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
set.seed(1234)

Set parameters

n_id <- 1000
n_snp <- 10
g <- matrix(rbinom(n_id*n_snp, 2, 0.4), n_id, n_snp)
n_age <- 30
beta <- matrix(rnorm(n_snp * 2), n_snp, 2)
beta_xy1 <- 1
beta_xy2 <- -0.3

Simulate x

dat <- lapply(
    1:n_age, \(i) {
        dat <- tibble(
            id = 1:n_id,
            age = i,
            score1 = g %*% beta[,1] %>% drop(),
            score2 = g %*% beta[,2] %>% drop(),
            x = case_when(
                age < 15 ~ rnorm(n_id) + score1,
                TRUE ~ rnorm(n_id) + score2
            )
        )
    }
) %>% bind_rows()
dat
# A tibble: 30,000 × 5
      id   age score1 score2      x
   <int> <int>  <dbl>  <dbl>  <dbl>
 1     1     1 -0.228 -0.100  0.478
 2     2     1 -0.795 -0.700 -0.510
 3     3     1 -0.144  0.972 -0.329
 4     4     1 -1.74   0.505 -3.27 
 5     5     1  3.26  -5.00   3.30 
 6     6     1  3.47  -4.85   2.78 
 7     7     1  2.78  -1.75   2.12 
 8     8     1  5.40  -4.74   6.29 
 9     9     1  1.50   0.976  2.38 
10    10     1  0.295  2.22   0.662
# ℹ 29,990 more rows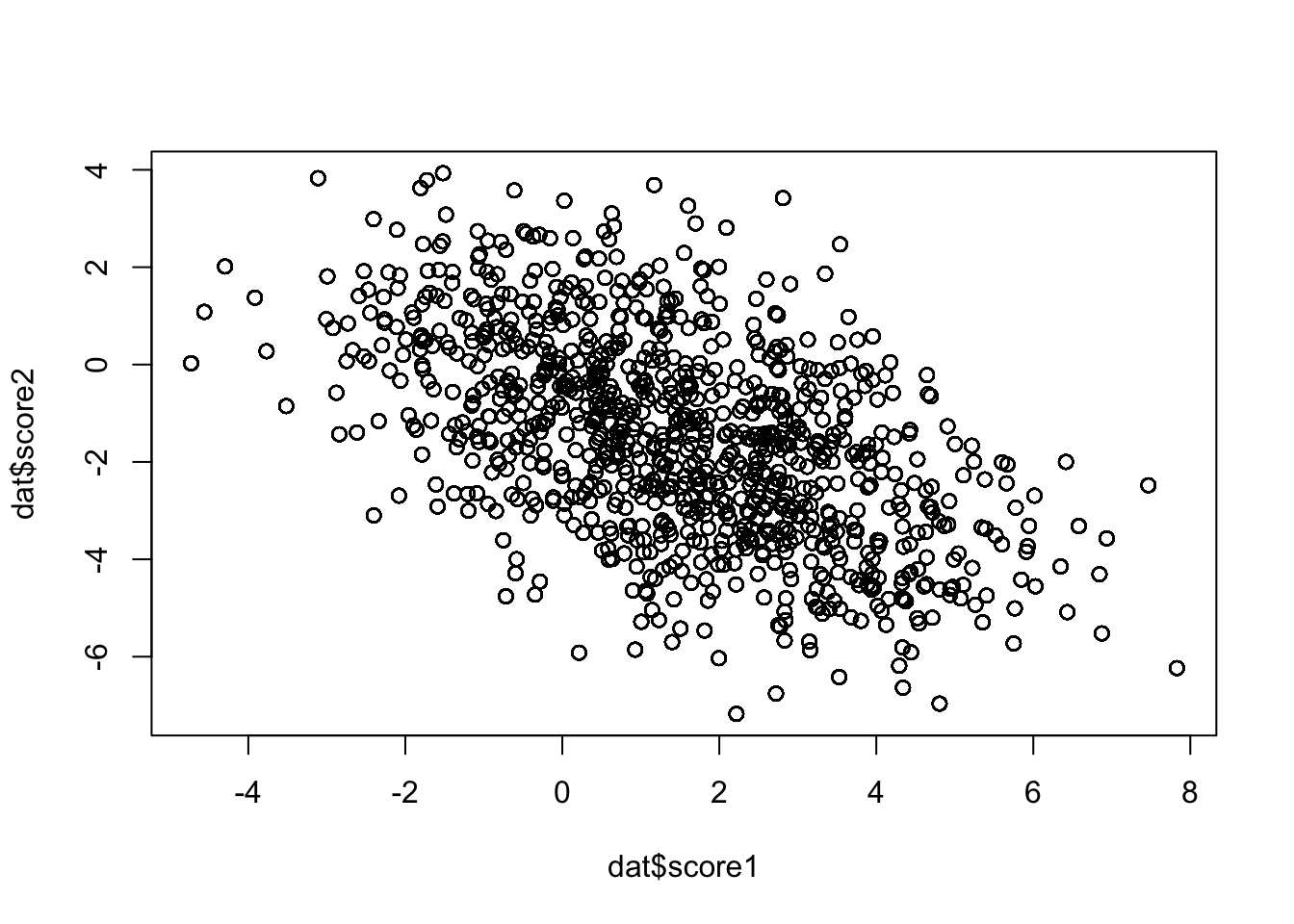
plot(dat$score1, dat$score2)

Simulate y

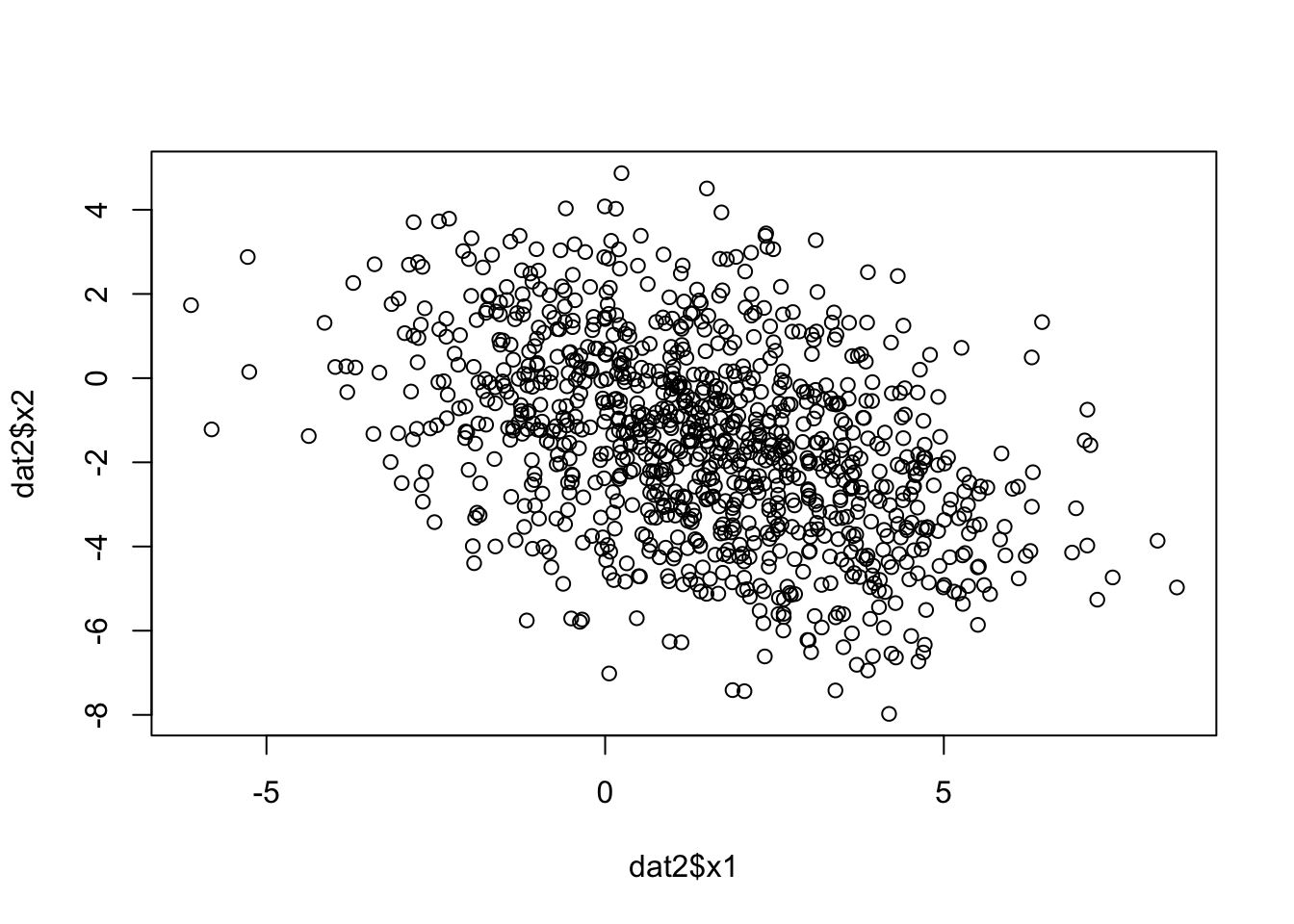
dat2 <- tibble(id = 1:n_id, x1 = subset(dat, age == 12)$x, x2 = subset(dat, age == 24)$x, y = x1 * beta_xy1 + x2 * beta_xy2 + rnorm(n_id))
plot(dat2$x1, dat2$x2)

Estimation of gx

dats <- dat %>% group_by(id) %>% slice_sample(n=1)
gx <- lapply(1:n_snp, \(i) {
    summary(lm(x ~ g[,i] * age, data=dats))$coef[c(2, 4), ] %>%
    as_tibble() %>%
    mutate(what=c("main", "interaction"))
}) %>% bind_rows()
gx
# A tibble: 20 × 5
   Estimate `Std. Error` `t value` `Pr(>|t|)` what       
      <dbl>        <dbl>     <dbl>      <dbl> <chr>      
 1 -1.06          0.218     -4.86    1.35e- 6 main       
 2  0.0613        0.0124     4.94    8.99e- 7 interaction
 3  0.219         0.228      0.959   3.38e- 1 main       
 4  0.00270       0.0131     0.206   8.37e- 1 interaction
 5 -1.41          0.217     -6.49    1.37e-10 main       
 6  0.0941        0.0124     7.60    6.86e-14 interaction
 7 -0.468         0.222     -2.11    3.53e- 2 main       
 8  0.00321       0.0126     0.255   7.99e- 1 interaction
 9 -0.336         0.219     -1.53    1.25e- 1 main       
10 -0.0178        0.0121    -1.47    1.41e- 1 interaction
11  0.760         0.226      3.37    7.79e- 4 main       
12  0.00458       0.0126     0.363   7.16e- 1 interaction
13  1.93          0.216      8.91    2.47e-18 main       
14 -0.0902        0.0123    -7.31    5.47e-13 interaction
15 -0.427         0.239     -1.78    7.46e- 2 main       
16  0.0175        0.0136     1.29    1.99e- 1 interaction
17  0.716         0.223      3.21    1.39e- 3 main       
18 -0.0582        0.0126    -4.61    4.57e- 6 interaction
19  2.89          0.187     15.5     1.04e-48 main       
20 -0.211         0.0107   -19.8     1.37e-73 interaction
gxm <- lapply(1:n_snp, \(i) {
    summary(lm(x ~ g[,i], data=dats))$coef %>%
    as_tibble() %>% slice_tail(n=1)
}) %>% bind_rows()
gxm
# A tibble: 10 × 4
   Estimate `Std. Error` `t value` `Pr(>|t|)`
      <dbl>        <dbl>     <dbl>      <dbl>
 1  -0.0135        0.120    -0.112   9.11e- 1
 2   0.234         0.124     1.89    5.95e- 2
 3  -0.0457        0.121    -0.377   7.06e- 1
 4  -0.385         0.120    -3.22    1.32e- 3
 5  -0.600         0.119    -5.04    5.53e- 7
 6   0.797         0.121     6.60    6.75e-11
 7   0.465         0.122     3.83    1.38e- 4
 8  -0.174         0.124    -1.41    1.60e- 1
 9  -0.181         0.122    -1.48    1.39e- 1
10  -0.377         0.121    -3.11    1.91e- 3

Estimation of gy

gy <- lapply(1:n_snp, \(i) {
    summary(lm(y ~ g[,i], data=dat2))$coef %>%
    as_tibble() %>% slice_tail(n=1)
}) %>% bind_rows()
gy
# A tibble: 10 × 4
   Estimate `Std. Error` `t value` `Pr(>|t|)`
      <dbl>        <dbl>     <dbl>      <dbl>
 1   -1.23         0.120    -10.3    1.11e-23
 2    0.248        0.130      1.91   5.69e- 2
 3   -1.22         0.121    -10.1    8.70e-23
 4   -0.442        0.125     -3.53   4.34e- 4
 5   -0.301        0.126     -2.38   1.73e- 2
 6    0.517        0.128      4.03   6.03e- 5
 7    1.44         0.120     12.0    3.86e-31
 8   -0.492        0.129     -3.81   1.50e- 4
 9    1.03         0.124      8.29   3.71e-16
10    2.30         0.105     22.0    1.90e-87

Univariable MR

summary(lm(gy$Estimate ~ gxm$Estimate, weight=1/gy$`Std. Error`^2))

Call:
lm(formula = gy$Estimate ~ gxm$Estimate, weights = 1/gy$`Std. Error`^2)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-12.552  -5.469  -2.040   4.930  20.153 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.2739     0.4130   0.663    0.526
gxm$Estimate   0.2270     1.0380   0.219    0.832

Residual standard error: 10.62 on 8 degrees of freedom
Multiple R-squared:  0.005941,  Adjusted R-squared:  -0.1183 
F-statistic: 0.04782 on 1 and 8 DF,  p-value: 0.8324

Multivariable MR

summary(lm(gy$Estimate ~ gx$Estimate[gx$what=="main"] + gx$Estimate[gx$what=="interaction"], weight=1/gy$`Std. Error`^2))

Call:
lm(formula = gy$Estimate ~ gx$Estimate[gx$what == "main"] + gx$Estimate[gx$what == 
    "interaction"], weights = 1/gy$`Std. Error`^2)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-2.3296 -0.7207 -0.0687  0.2519  3.7992 

Coefficients:
                                      Estimate Std. Error t value Pr(>|t|)   
(Intercept)                           -0.06306    0.07384  -0.854  0.42137   
gx$Estimate[gx$what == "main"]         0.77715    0.17219   4.513  0.00275 **
gx$Estimate[gx$what == "interaction"] -1.09444    2.64623  -0.414  0.69155   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.827 on 7 degrees of freedom
Multiple R-squared:  0.9743,    Adjusted R-squared:  0.9669 
F-statistic: 132.5 on 2 and 7 DF,  p-value: 2.733e-06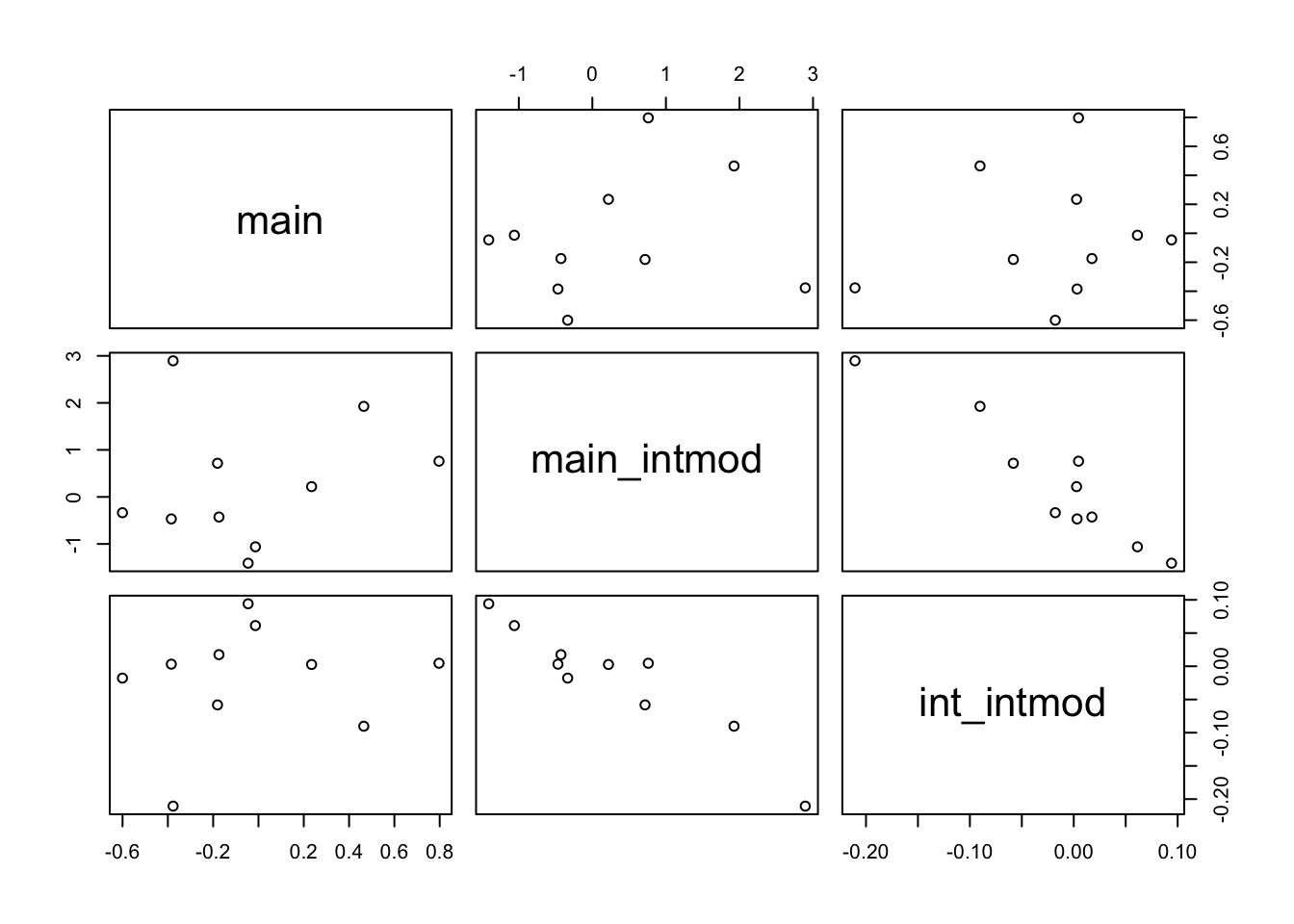
tibble(
    main = gxm$Estimate,
    main_intmod = gx$Estimate[gx$what=="main"],
    int_intmod = gx$Estimate[gx$what=="interaction"]
) %>% plot()

Univariable MR using only main effect from interaction model

summary(lm(gy$Estimate ~ gx$Estimate[gx$what=="main"] + gx$Estimate[gx$what=="interaction"], weight=1/gy$`Std. Error`^2))

Call:
lm(formula = gy$Estimate ~ gx$Estimate[gx$what == "main"] + gx$Estimate[gx$what == 
    "interaction"], weights = 1/gy$`Std. Error`^2)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-2.3296 -0.7207 -0.0687  0.2519  3.7992 

Coefficients:
                                      Estimate Std. Error t value Pr(>|t|)   
(Intercept)                           -0.06306    0.07384  -0.854  0.42137   
gx$Estimate[gx$what == "main"]         0.77715    0.17219   4.513  0.00275 **
gx$Estimate[gx$what == "interaction"] -1.09444    2.64623  -0.414  0.69155   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.827 on 7 degrees of freedom
Multiple R-squared:  0.9743,    Adjusted R-squared:  0.9669 
F-statistic: 132.5 on 2 and 7 DF,  p-value: 2.733e-06
summary(lm(gy$Estimate ~ gx$Estimate[gx$what=="interaction"], weight=1/gy$`Std. Error`^2))

Call:
lm(formula = gy$Estimate ~ gx$Estimate[gx$what == "interaction"], 
    weights = 1/gy$`Std. Error`^2)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-3.5825 -2.5945 -0.6845  2.9359  5.0269 

Coefficients:
                                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)                            -0.07095    0.13653  -0.520    0.617    
gx$Estimate[gx$what == "interaction"] -12.48205    1.47600  -8.457 2.92e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.379 on 8 degrees of freedom
Multiple R-squared:  0.8994,    Adjusted R-squared:  0.8868 
F-statistic: 71.52 on 1 and 8 DF,  p-value: 2.922e-05
summary(lm(gy$Estimate ~ gx$Estimate[gx$what=="main"], weight=1/gy$`Std. Error`^2))

Call:
lm(formula = gy$Estimate ~ gx$Estimate[gx$what == "main"], weights = 1/gy$`Std. Error`^2)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-2.3163 -0.7453 -0.2029  0.3130  3.8931 

Coefficients:
                               Estimate Std. Error t value Pr(>|t|)    
(Intercept)                    -0.05969    0.06948  -0.859    0.415    
gx$Estimate[gx$what == "main"]  0.84505    0.04916  17.190 1.33e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.73 on 8 degrees of freedom
Multiple R-squared:  0.9736,    Adjusted R-squared:  0.9703 
F-statistic: 295.5 on 1 and 8 DF,  p-value: 1.334e-07

Run a few different parameters

Make simulation and estimation functions from above

sim <- function(n_id, n_snp, n_age, beta_xy1, beta_xy2) {
    g <- matrix(rbinom(n_id*n_snp, 2, 0.4), n_id, n_snp)
    beta <- matrix(rnorm(n_snp * 2), n_snp, 2)
    dat <- lapply(
        1:n_age, \(i) {
            dat <- tibble(
                id = 1:n_id,
                age = i,
                score1 = g %*% beta[,1] %>% drop(),
                score2 = g %*% beta[,2] %>% drop(),
                x = case_when(
                    age < 15 ~ rnorm(n_id) + score1,
                    TRUE ~ rnorm(n_id) + score2
                )
            )
        }
    ) %>% bind_rows()

    dat2 <- tibble(id = 1:n_id, x1 = subset(dat, age == 12)$x, x2 = subset(dat, age == 24)$x, y = x1 * beta_xy1 + x2 * beta_xy2 + rnorm(n_id))
    dats <- dat %>% group_by(id) %>% slice_sample(n=1)
    gx <- lapply(1:n_snp, \(i) {
        summary(lm(x ~ g[,i] * age, data=dats))$coef[c(2, 4), ] %>%
        as_tibble() %>%
        mutate(what=c("main", "interaction"))
    }) %>% bind_rows()

    gxm <- lapply(1:n_snp, \(i) {
        summary(lm(x ~ g[,i], data=dats))$coef %>%
        as_tibble() %>% slice_tail(n=1)
    }) %>% bind_rows()

    gy <- lapply(1:n_snp, \(i) {
        summary(lm(y ~ g[,i], data=dat2))$coef %>%
        as_tibble() %>% slice_tail(n=1)
    }) %>% bind_rows()

    return(list(gy=gy, gx=gx, gxm=gxm))
}

estimation <- function(ests) {
    return(list(
        main = with(ests, summary(lm(gy$Estimate ~ 0 + gxm$Estimate, weight=1/gy$`Std. Error`^2))$coef),
        full = with(ests, summary(lm(gy$Estimate ~ 0 + gx$Estimate[gx$what=="main"] + gx$Estimate[gx$what=="interaction"], weight=1/gy$`Std. Error`^2))$coef),
        int_main = with(ests, summary(lm(gy$Estimate ~ 0 + gx$Estimate[gx$what=="main"], weight=1/gy$`Std. Error`^2))$coef),
        int_int = with(ests, summary(lm(gy$Estimate ~ 0 + gx$Estimate[gx$what=="interaction"], weight=1/gy$`Std. Error`^2))$coef)
    ))
}

Null model

sim(n_id=1000, n_snp=10, n_age=30, beta_xy1=0, beta_xy2=0) %>% estimation
$main
                Estimate Std. Error   t value  Pr(>|t|)
gxm$Estimate -0.03131924 0.02202768 -1.421813 0.1887952

$full
                                        Estimate Std. Error    t value
gx$Estimate[gx$what == "main"]        -0.0235155 0.02371966 -0.9913928
gx$Estimate[gx$what == "interaction"] -0.1510470 0.46080124 -0.3277921
                                       Pr(>|t|)
gx$Estimate[gx$what == "main"]        0.3505285
gx$Estimate[gx$what == "interaction"] 0.7514828

$int_main
                                  Estimate  Std. Error   t value  Pr(>|t|)
gx$Estimate[gx$what == "main"] -0.01642267 0.009222158 -1.780784 0.1086416

$int_int
                                       Estimate Std. Error  t value  Pr(>|t|)
gx$Estimate[gx$what == "interaction"] 0.2656993  0.1885832 1.408923 0.1924575

No associations at any model

Same effect at each time point

sim(n_id=1000, n_snp=10, n_age=30, beta_xy1=1, beta_xy2=1) %>% estimation
$main
             Estimate Std. Error  t value     Pr(>|t|)
gxm$Estimate 2.210015  0.1139279 19.39837 1.188461e-08

$full
                                       Estimate Std. Error  t value
gx$Estimate[gx$what == "main"]         2.066242 0.06113766 33.79655
gx$Estimate[gx$what == "interaction"] 29.105622 1.39147350 20.91712
                                          Pr(>|t|)
gx$Estimate[gx$what == "main"]        6.416918e-10
gx$Estimate[gx$what == "interaction"] 2.863315e-08

$int_main
                               Estimate Std. Error  t value    Pr(>|t|)
gx$Estimate[gx$what == "main"] 1.025186  0.2498177 4.103738 0.002661794

$int_int
                                       Estimate Std. Error   t value  Pr(>|t|)
gx$Estimate[gx$what == "interaction"] -9.177769   9.135675 -1.004608 0.3413298

Main effect as expected, interaction term is there because of accumulated effect?

No effect at second time point

sim(n_id=10000, n_snp=10, n_age=30, beta_xy1=1, beta_xy2=0) %>% estimation
$main
              Estimate Std. Error  t value   Pr(>|t|)
gxm$Estimate 0.7739871  0.2630003 2.942913 0.01640885

$full
                                       Estimate Std. Error  t value
gx$Estimate[gx$what == "main"]        0.9913733 0.01897743 52.23960
gx$Estimate[gx$what == "interaction"] 4.9867301 0.32304742 15.43653
                                          Pr(>|t|)
gx$Estimate[gx$what == "main"]        1.998216e-11
gx$Estimate[gx$what == "interaction"] 3.084458e-07

$int_main
                                Estimate Std. Error  t value     Pr(>|t|)
gx$Estimate[gx$what == "main"] 0.7830066 0.06978057 11.22098 1.361042e-06

$int_int
                                       Estimate Std. Error   t value  Pr(>|t|)
gx$Estimate[gx$what == "interaction"] -7.016759    3.95985 -1.771976 0.1101626

Almost no interaction effect

No effect at first time point

sim(n_id=10000, n_snp=10, n_age=30, beta_xy1=0, beta_xy2=1) %>% estimation
$main
             Estimate Std. Error  t value  Pr(>|t|)
gxm$Estimate 1.084445    0.37676 2.878345 0.0182271

$full
                                       Estimate Std. Error  t value
gx$Estimate[gx$what == "main"]         1.016923 0.02454421 41.43228
gx$Estimate[gx$what == "interaction"] 25.108538 0.42035475 59.73178
                                          Pr(>|t|)
gx$Estimate[gx$what == "main"]        1.268347e-10
gx$Estimate[gx$what == "interaction"] 6.856027e-12

$int_main
                                 Estimate Std. Error   t value  Pr(>|t|)
gx$Estimate[gx$what == "main"] -0.2712219  0.2336052 -1.161027 0.2754984

$int_int
                                      Estimate Std. Error  t value    Pr(>|t|)
gx$Estimate[gx$what == "interaction"] 9.805954   2.778471 3.529263 0.006421374

Only shows an interaction effect.

Summary

No idea what is going on. This model is probably too simple, doesn’t include auto-correlation in x across age.

sessionInfo()
R version 4.4.1 (2024-06-14)
Platform: aarch64-apple-darwin20
Running under: macOS Sonoma 14.6.1

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.4-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] dplyr_1.1.4

loaded via a namespace (and not attached):
 [1] digest_0.6.37     utf8_1.2.4        R6_2.5.1          fastmap_1.2.0    
 [5] tidyselect_1.2.1  xfun_0.48         magrittr_2.0.3    glue_1.8.0       
 [9] tibble_3.2.1      knitr_1.48        pkgconfig_2.0.3   htmltools_0.5.8.1
[13] rmarkdown_2.27    generics_0.1.3    lifecycle_1.0.4   cli_3.6.3        
[17] fansi_1.0.6       vctrs_0.6.5       compiler_4.4.1    tools_4.4.1      
[21] pillar_1.9.0      evaluate_1.0.1    yaml_2.3.10       rlang_1.1.4      
[25] jsonlite_1.8.9    htmlwidgets_1.6.4