Type 2 diabetes risk differences between populations

Author

Gibran Hemani

Published

November 21, 2023

Background

T2D rates are ~5x higher amongst South Asians than native British populations in Britain. Most likely due to environmental differences, but could it hypothetically be explained by differences in genetic architecture?

Assume polygenic common variant distribution and a disease liability threshold model.

Descriptive statistice

  • t2d diagnosis normally 45-65
  • people aged 45+ constitute approx 50% of 70 million people
  • therefore 4.9 million t2d cases in uk out of 35 million people who are susceptible
  • 3.07 million South Asians, assume 50% aged 45+
  • Prevalence is 5x higher amongst South Asians

Simultaneous equations:

\[ 4.9 = 1.54 x + 35y \]

where \(x\) is the prevalence amongst South Asians and \(y\) is the prevalence amongst white British

Also

\[ x = y * 5 \]

Calculate prevalences:

A <- matrix(c(1.54, 35, -1, 5), nrow=2, byrow=T)
b <- c(4.9, 0)
prev <- solve(A, b)
prev
[1] 0.5737705 0.1147541

Model

Assume threshold is the same in both populations. Establish a threshold based on European genetic architecture

library(ggplot2)
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
sim1 <- function(mg, vg, me, ve, prev) {
    n <- 100000
    g <- rnorm(n, mg, sqrt(vg))
    e <- rnorm(n, me, sqrt(ve))
    l <- g + e
    thresh <- quantile(l, 1-prev)
    return(thresh)
}

thresh <- sim1(0, 0.4, 0, 0.6, prev[2])
thresh
88.52459% 
 1.204965

Estimate prevalence given a threshold when parameters change

sim2 <- function(mg, vg, me, ve, thresh) {
    n <- 100000
    g <- rnorm(n, mg, sqrt(vg))
    e <- rnorm(n, me, sqrt(ve))
    l <- g + e
    prev <- sum(l > thresh) / n
    return(prev)
}

sim2(0.1, 0.4, 0, 0.6, thresh)
[1] 0.13381

Enumerate possibilities

param <- expand.grid(
    mg = seq(0, 4, by=0.01),
    vg = 0.4,
    me = 0,
    ve = 0.6,
    thresh = thresh,
    prev = NA
)

for(i in 1:nrow(param)) {
    param$prev[i] <- sim2(param$mg[i], param$vg[i], param$me[i], param$ve[i], param$thresh[i])
}

param$ratio = param$prev / prev[2]

ggplot(param, aes(x=mg, y=ratio)) +
geom_line() +
geom_hline(yintercept=5, linetype="dotted")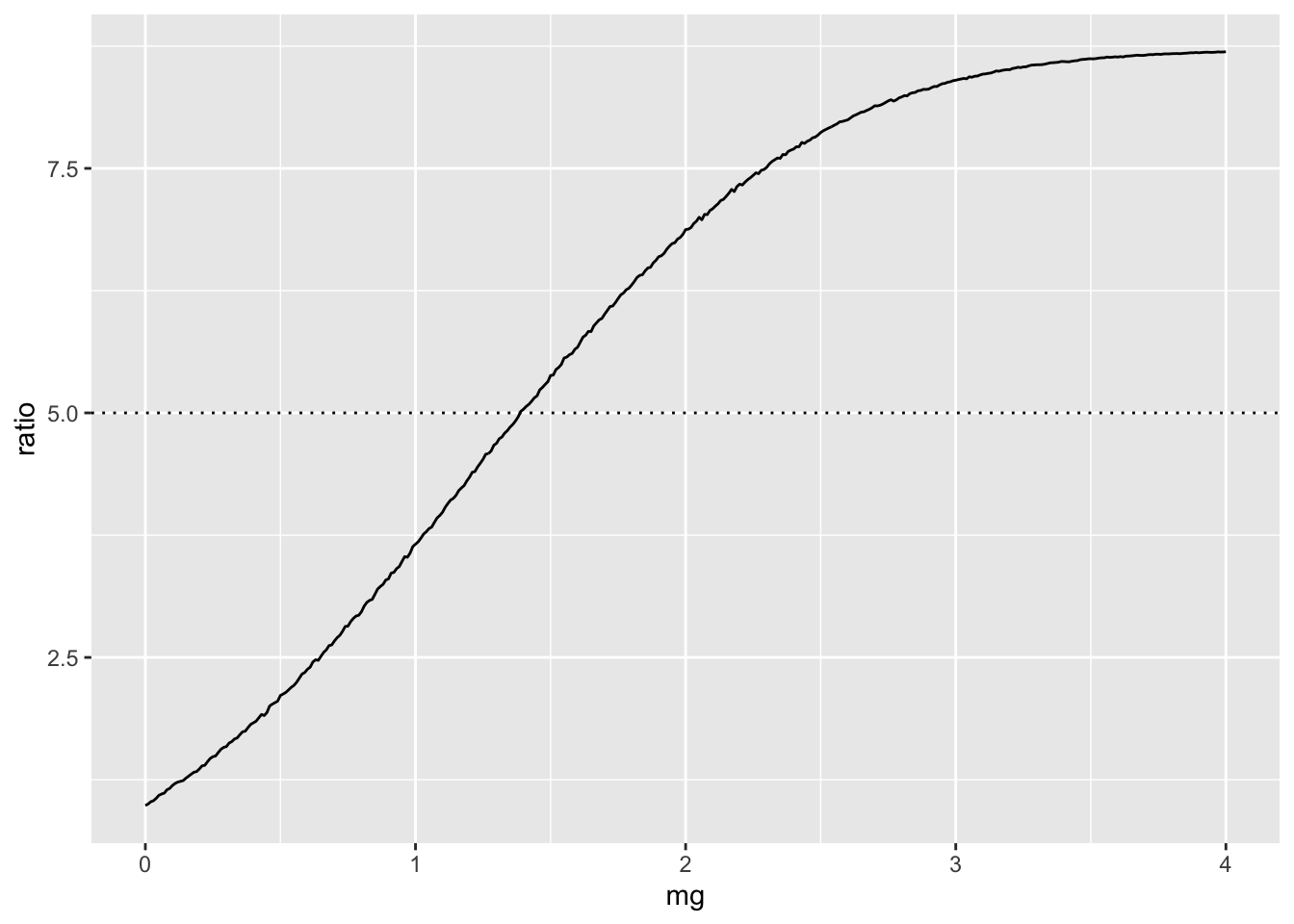

This shows how much larger the mean of the genetic liability would have to be to lead to 5x prevalence

Comparison of distributions:

mg <- param$mg[which(param$ratio >= 5)[1]]
bind_rows(
    tibble(pop="EUR", x=seq(-3, 3, length.out=1000), val = dnorm(x, sd=sqrt(0.4))),
    tibble(pop="SAS", x=seq(-3+mg, 3+mg, length.out=1000), val = dnorm(x, m=mg, sd=sqrt(0.4)))
) %>% ggplot(., aes(x=x, y=val)) +
geom_line(aes(colour=pop)) +
geom_vline(xintercept=thresh)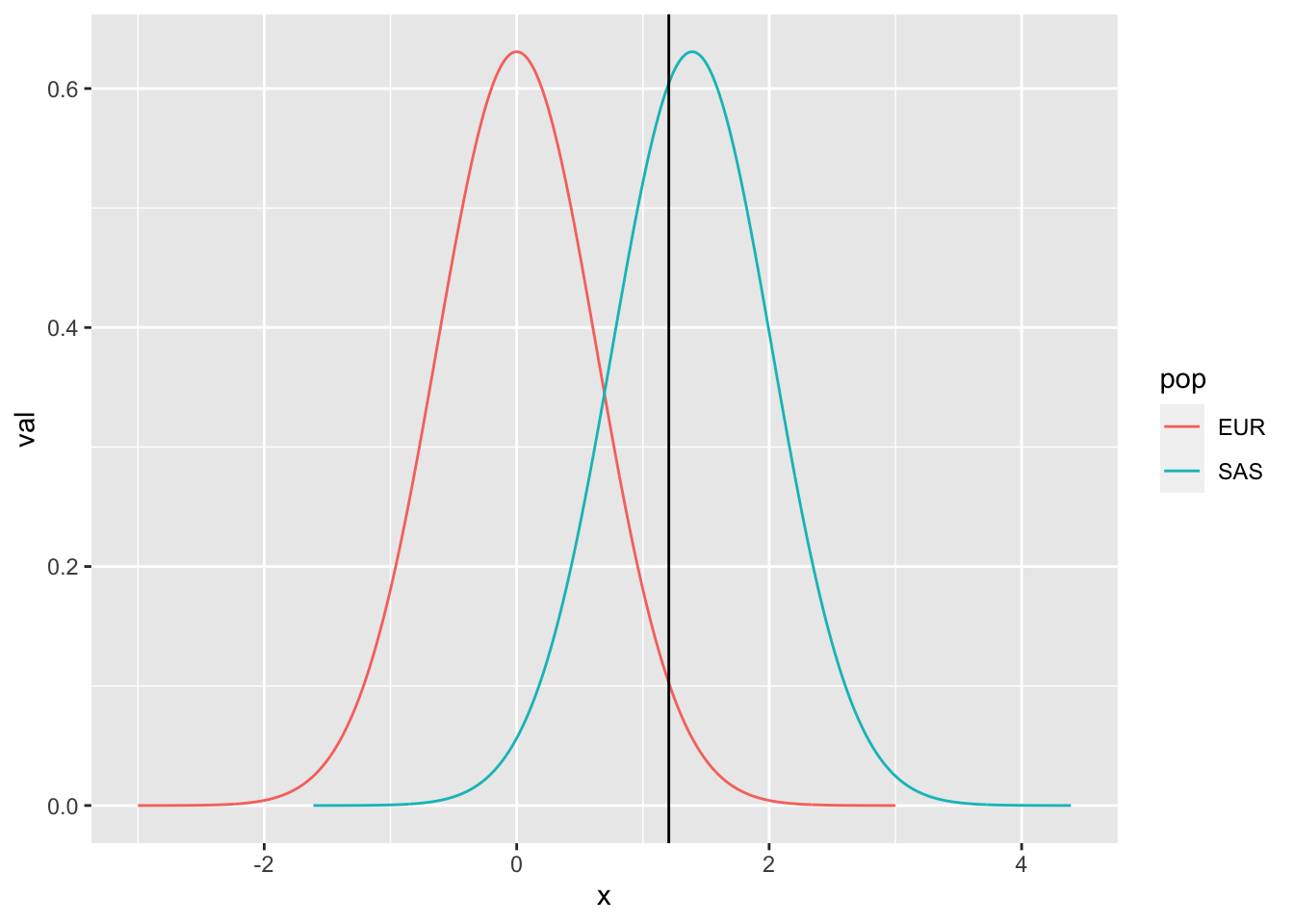

Is it plausible in terms of just different allele frequencies?

nsnp <- 10000
af <- rbeta(nsnp, 1, 1) / 2
hist(af)

b <- rnorm(nsnp, 0, (2*af*(1-af))^-0.4)
vg <- sum(b^2 * 2 * af * (1-af))
b <- b / sqrt(vg) * 0.4
plot(b ~ af)

nid <- 1000
g1 <- sapply(af, \(x) { rbinom(nid, 2, x) })
score1 <- g1 %*% b
hist(score1)

sd(score1)
[1] 0.383443

Summary

  • Seems unlikely under this model
sessionInfo()
R version 4.3.2 (2023-10-31)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Ventura 13.6

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] dplyr_1.1.4   ggplot2_3.4.2

loaded via a namespace (and not attached):
 [1] vctrs_0.6.4       cli_3.6.1         knitr_1.45        rlang_1.1.2      
 [5] xfun_0.41         generics_0.1.3    jsonlite_1.8.7    labeling_0.4.2   
 [9] glue_1.6.2        colorspace_2.1-0  htmltools_0.5.7   scales_1.2.1     
[13] fansi_1.0.5       rmarkdown_2.25    grid_4.3.2        evaluate_0.23    
[17] munsell_0.5.0     tibble_3.2.1      fastmap_1.1.1     yaml_2.3.7       
[21] lifecycle_1.0.4   compiler_4.3.2    htmlwidgets_1.6.3 pkgconfig_2.0.3  
[25] farver_2.1.1      digest_0.6.33     R6_2.5.1          tidyselect_1.2.0 
[29] utf8_1.2.4        pillar_1.9.0      magrittr_2.0.3    withr_2.5.2      
[33] tools_4.3.2       gtable_0.3.3