Age interactions

GxE
Author

Gibran Hemani

Published

October 5, 2023

Background

We can infer the age-specific effect of trait-variant association in various ways. How do they relate? e.g.

  • Stratify individuals by age group and get the main effect
  • Fit age as an interaction term
  • 2-step linear model - get per-individual age slopes and intercepts, estimate genetic effects on slopes and parameters

Age isn’t a collider so stratifying shouldn’t introduce problems.

Approach - each individual has a growth curve with parameters that are genetically influenced. What happens when we age stratify using different methods?

library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(ggplot2)
library(lme4)
Loading required package: Matrix
set.seed(1234)

Simulate data

growth_curve2 <- function(x, phi1=20, phi2=-2.4, phi3=0.3) {
    g <- phi1 / (1 + exp(-(phi2 + phi3 * x)))
    g + rnorm(length(g), sd=g/(max(g)*10))
}

nid <- 50000

bg1 <- 5/2
bg2 <- 0.1/2
pg1 <- 0.3
pg2 <- 0.3

bmi <- lapply(1:nid, function(i) {
    tibble(
        id=i,
        g1 = rbinom(1, 2, pg1),
        g2 = rbinom(1, 2, pg2),
        age=sample(0:50, 20, replace=FALSE),
        value=growth_curve2(age, g1 * bg1 + rnorm(1, mean=23, sd=5), -2.4, g2 * bg2 + rnorm(1, mean=0.3, sd=0.1))
    ) %>% arrange(age)
}) %>% bind_rows()

str(bmi)
tibble [1,000,000 × 5] (S3: tbl_df/tbl/data.frame)
 $ id   : int [1:1000000] 1 1 1 1 1 1 1 1 1 1 ...
 $ g1   : int [1:1000000] 0 0 0 0 0 0 0 0 0 0 ...
 $ g2   : int [1:1000000] 1 1 1 1 1 1 1 1 1 1 ...
 $ age  : int [1:1000000] 3 4 5 8 13 14 15 20 21 25 ...
 $ value: num [1:1000000] 4.03 4.72 5.49 8.35 14.52 ...

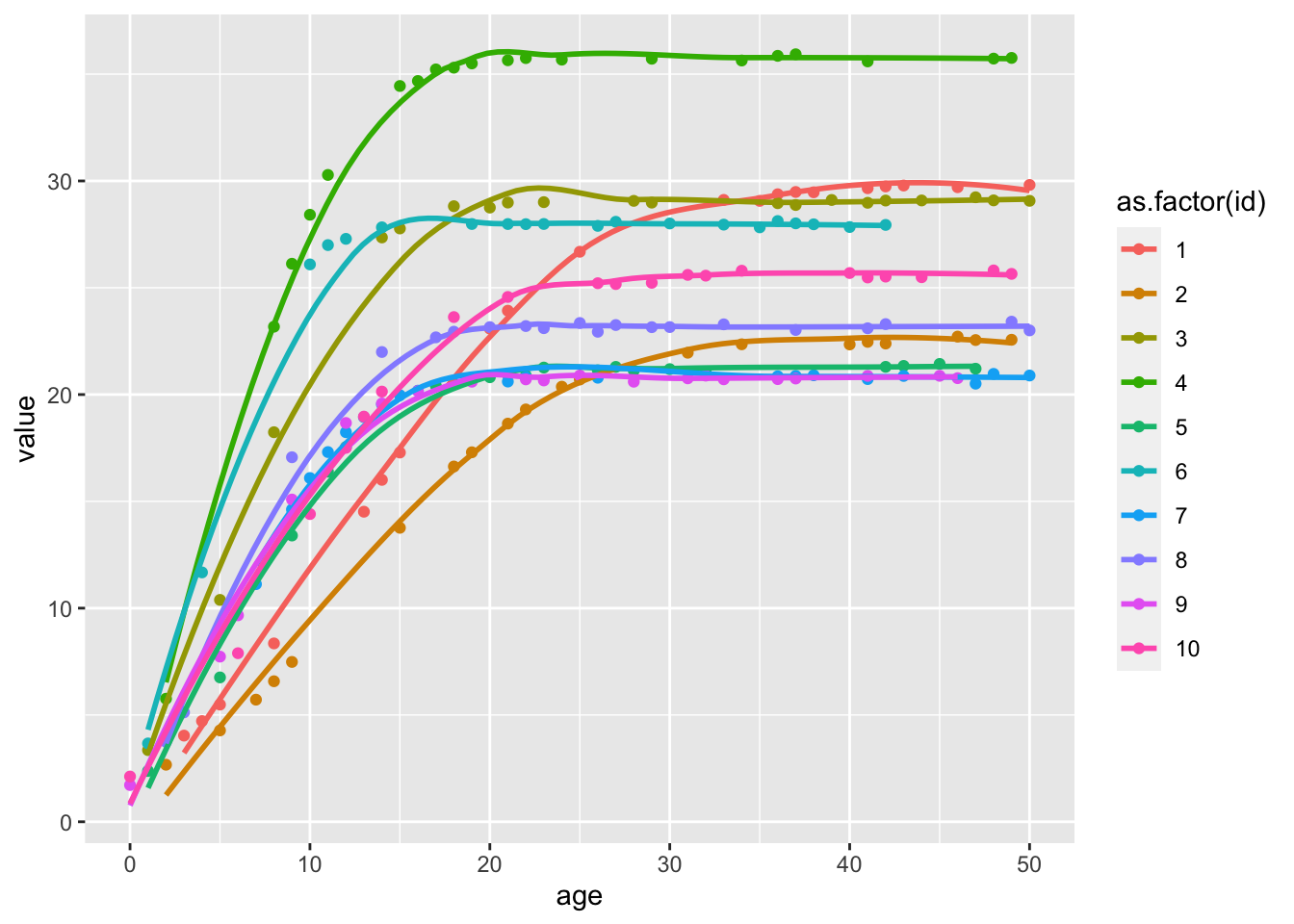
Example of what simulated data looks like

ggplot(bmi %>% filter(id < 11), aes(x=age, y=value)) +
geom_point(aes(colour=as.factor(id))) +
geom_smooth(aes(colour=as.factor(id)), se=FALSE)
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'

Stratifying by age, and getting main effect in each stratum

o <- lapply(unique(bmi$age), function(a) {
  x <- subset(bmi, age == a) %>% slice_sample(n=1000)
  print(dim(x))
  r <- bind_rows(
    summary(lm(value ~ g1, x))$coef %>% as_tibble() %>% mutate(g=1) %>% slice_tail(n=1),
    summary(lm(value ~ g2, x))$coef %>% as_tibble() %>% mutate(g=2) %>% slice_tail(n=1)
  )
  names(r) <- c("beta", "se", "tval", "pval", "g")
  r$age <- a
  return(r)
}) %>% bind_rows()
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
[1] 1000    5
o
# A tibble: 102 × 6
    beta     se  tval     pval     g   age
   <dbl>  <dbl> <dbl>    <dbl> <dbl> <int>
 1 0.578 0.0753  7.68 3.88e-14     1     3
 2 0.653 0.0750  8.71 1.28e-17     2     3
 3 0.481 0.114   4.21 2.82e- 5     1     4
 4 1.08  0.117   9.17 2.57e-19     2     4
 5 1.13  0.164   6.91 8.44e-12     1     5
 6 1.46  0.163   8.92 2.25e-18     2     5
 7 1.59  0.257   6.17 9.71e-10     1     8
 8 1.67  0.250   6.67 4.32e-11     2     8
 9 2.52  0.286   8.81 5.51e-18     1    13
10 1.40  0.297   4.71 2.85e- 6     2    13
# ℹ 92 more rows
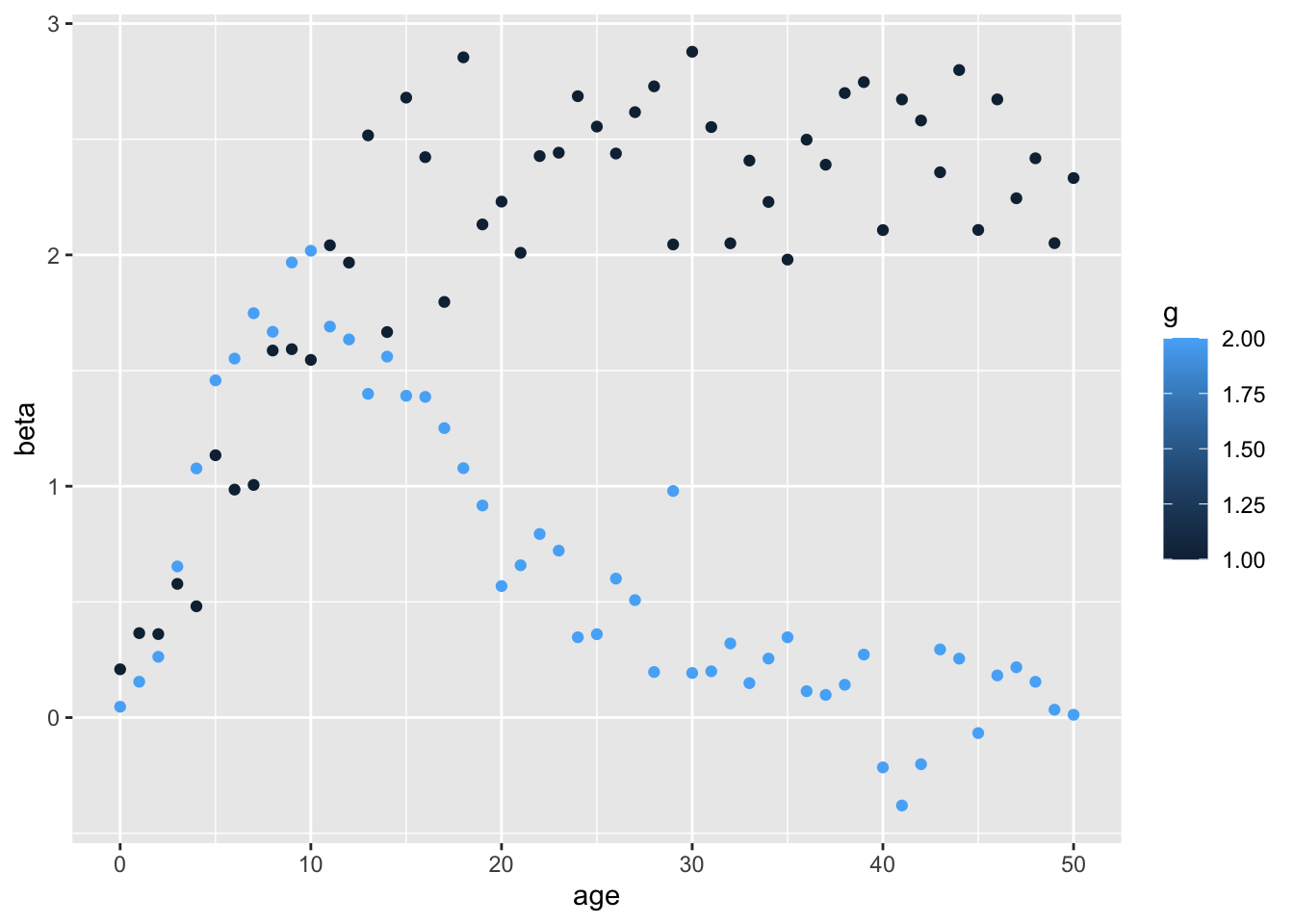
ggplot(o, aes(y=beta, x= age)) +
  geom_point(aes(colour=g))

Makes sense because g1 influences the asymptote, and g2 influences the rate of growth.

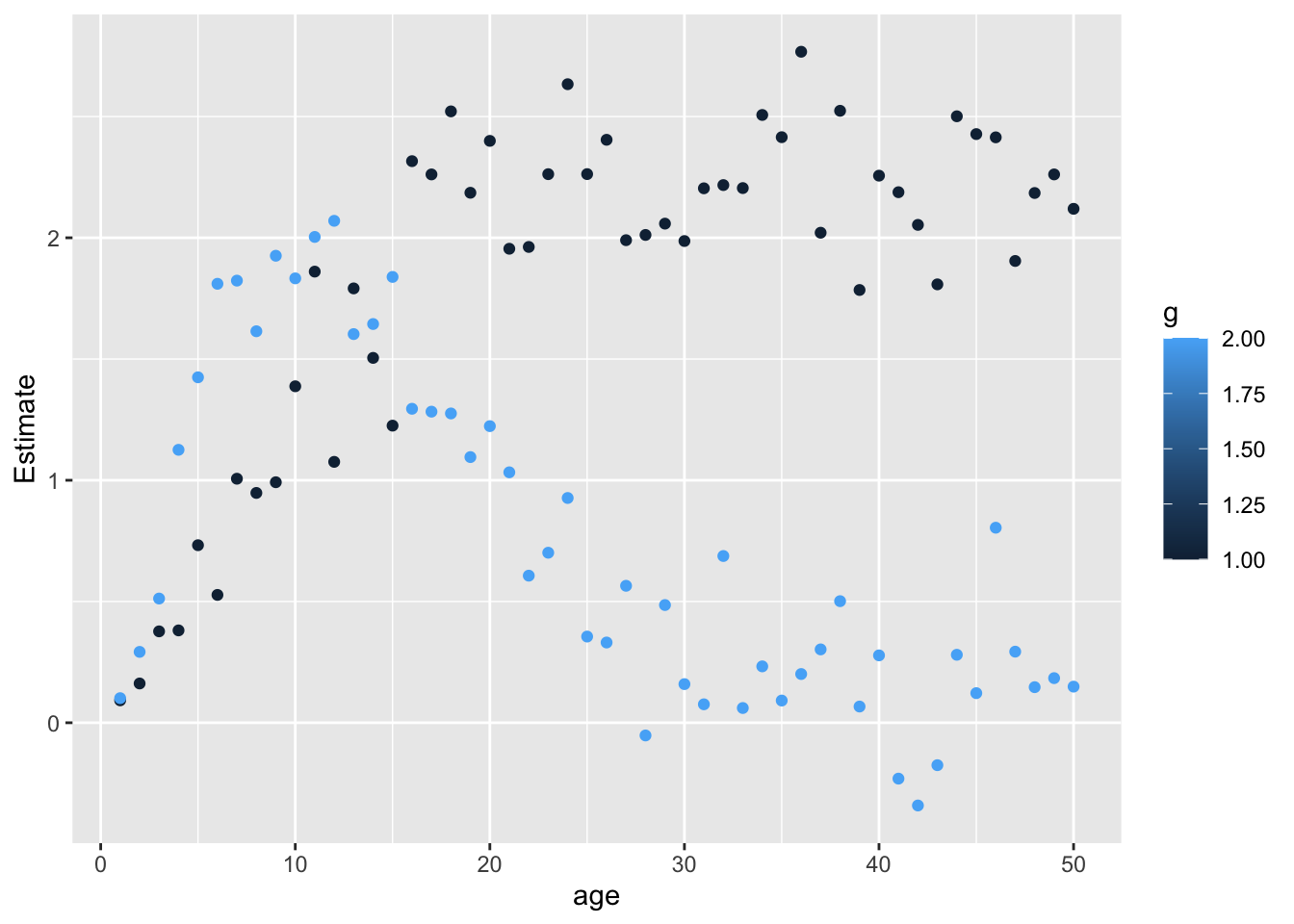
Interaction with main effect - does it give the same thing?

oi1 <- bmi %>% group_by(id) %>%
  slice_sample(n=1) %>%
  {summary(lm(value ~ g1 * as.factor(age), .))$coef}
oi2 <- bmi %>% group_by(id) %>%
  slice_sample(n=1) %>%
  {summary(lm(value ~ g2 * as.factor(age), .))$coef}
oi1 <- bind_cols(p = rownames(oi1), oi1) %>% as_tibble %>% filter(grepl("g1:", p)) %>% mutate(age=gsub("g1\\:as.factor\\(age\\)", "", p) %>% as.numeric(), g=1)
oi2 <- bind_cols(p = rownames(oi2), oi2) %>% as_tibble %>% filter(grepl("g2:", p)) %>% mutate(age=gsub("g2\\:as.factor\\(age\\)", "", p) %>% as.numeric(), g=2)

ggplot(bind_rows(oi1, oi2), aes(y=Estimate, x=age)) +
  geom_point(aes(colour=g))

Linear model for each individual

temp <- bmi %>% filter(id %in% 1:1000)
a <- lmer(value ~ age + (1+age|id), data=temp)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0579551 (tol = 0.002, component 1)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model is nearly unidentifiable: very large eigenvalue
 - Rescale variables?
b <- ranef(a)
head(b$id)
  (Intercept)          age
1 -3.11384947  0.164278524
2 -4.39460900  0.033832734
3  4.75739472 -0.012807851
4 11.70591067  0.013564999
5 -0.06871647 -0.050490788
6  5.65167436 -0.005632972
rbind(
    summary(lm(b$id[,1] ~ temp$g1[!duplicated(temp$id)]))$coef[2,],
    summary(lm(b$id[,2] ~ temp$g1[!duplicated(temp$id)]))$coef[2,],
    summary(lm(b$id[,1] ~ temp$g2[!duplicated(temp$id)]))$coef[2,],
    summary(lm(b$id[,2] ~ temp$g2[!duplicated(temp$id)]))$coef[2,]
)
        Estimate  Std. Error   t value     Pr(>|t|)
[1,]  1.05784708 0.194558484  5.437168 6.807184e-08
[2,]  0.02622162 0.004303497  6.093097 1.579452e-09
[3,]  1.30851566 0.195321406  6.699295 3.493596e-11
[4,] -0.02265172 0.004374294 -5.178370 2.706779e-07

Summary

  • Stratifying by age gives same result as fitting age as an interaction - provided that interaction includes main effects for snp and age
  • Linear model still picks things up

Experiment - interactions with a collider

If there is a binary variable that is a collider, does it make a difference if it is tested stratified or as an interaction term

note this isn’t an issue for age which can’t be a collider

n <- 10000
x <- rnorm(n)
y <- rnorm(n)
u <- x + y + rnorm(n)
C <- rbinom(n, 1, plogis(u))
summary(lm(y ~ x, subset=C==1))$coef[2,1]
[1] -0.1274305
summary(lm(y ~ x, subset=C==0))$coef[2,1]
[1] -0.1197606
summary(lm(y ~ x))$coef[2,1]
[1] 0.003735308
summary(lm(y ~ x * as.factor(C)))

Call:
lm(formula = y ~ x * as.factor(C))

Residuals:
    Min      1Q  Median      3Q     Max 
-3.6992 -0.6213 -0.0028  0.6146  3.3290 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)     -0.37280    0.01379 -27.034   <2e-16 ***
x               -0.11976    0.01423  -8.415   <2e-16 ***
as.factor(C)1    0.74257    0.01964  37.802   <2e-16 ***
x:as.factor(C)1 -0.00767    0.01993  -0.385      0.7    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9241 on 9996 degrees of freedom
Multiple R-squared:  0.1251,    Adjusted R-squared:  0.1248 
F-statistic: 476.5 on 3 and 9996 DF,  p-value: < 2.2e-16
summary(lm(y ~ x : as.factor(C)))

Call:
lm(formula = y ~ x:as.factor(C))

Residuals:
    Min      1Q  Median      3Q     Max 
-4.0158 -0.6645 -0.0068  0.6616  3.2348 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
(Intercept)     -0.006836   0.010499  -0.651    0.515
x:as.factor(C)0  0.009325   0.014769   0.631    0.528
x:as.factor(C)1 -0.001655   0.014488  -0.114    0.909

Residual standard error: 0.988 on 9997 degrees of freedom
Multiple R-squared:  4.045e-05, Adjusted R-squared:  -0.0001596 
F-statistic: 0.2022 on 2 and 9997 DF,  p-value: 0.8169

Summary

  • interaction with a collider is a problem as expected
sessionInfo()
R version 4.3.0 (2023-04-21)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Ventura 13.5.2

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] lme4_1.1-33   Matrix_1.5-4  ggplot2_3.4.2 dplyr_1.1.2  

loaded via a namespace (and not attached):
 [1] gtable_0.3.3      jsonlite_1.8.7    compiler_4.3.0    Rcpp_1.0.10      
 [5] tidyselect_1.2.0  splines_4.3.0     scales_1.2.1      boot_1.3-28.1    
 [9] yaml_2.3.7        fastmap_1.1.1     lattice_0.21-8    R6_2.5.1         
[13] labeling_0.4.2    generics_0.1.3    knitr_1.43        htmlwidgets_1.6.2
[17] MASS_7.3-58.4     tibble_3.2.1      nloptr_2.0.3      munsell_0.5.0    
[21] minqa_1.2.5       pillar_1.9.0      rlang_1.1.1       utf8_1.2.3       
[25] xfun_0.39         cli_3.6.1         mgcv_1.8-42       withr_2.5.0      
[29] magrittr_2.0.3    digest_0.6.31     grid_4.3.0        rstudioapi_0.14  
[33] lifecycle_1.0.3   nlme_3.1-162      vctrs_0.6.3       evaluate_0.21    
[37] glue_1.6.2        farver_2.1.1      fansi_1.0.4       colorspace_2.1-0 
[41] rmarkdown_2.22    tools_4.3.0       pkgconfig_2.0.3   htmltools_0.5.5