IV confounding with changing variances

Author

Gibran Hemani

Published

July 20, 2023

Background

When instruments arise through U the bias is buy/bux, whereas ols bias is buy*bux. If buy is larger than bux then the iv bias will be smaller than ols bias, but otherwise likely to be larger than ols bias.

What happens if you just rescale the values of x and y?

bias_ols = buy * bux

When the SNP goes through U bias_iv = buy/bux

buy = 0.1 bux = 0.1

bias_iv = 1 bias_ols = 0.01

change sd of y and x to be from 1 to 10

buy = 1 bux = 1

bias_iv = 1 bias_ols = 1

buy = 0.1 bux = 1

bias_iv = 0.1 bias_ols = 0.1

y = buy * u + e x = bux * u + e

b_ols = cov(buyu, buxu) = buy * bux * var(u)

library(ggplot2)
library(tidyr)
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(TwoSampleMR)
TwoSampleMR version 0.5.7 
[>] New: Option to use non-European LD reference panels for clumping etc
[>] Some studies temporarily quarantined to verify effect allele
[>] See news(package='TwoSampleMR') and https://gwas.mrcieu.ac.uk for further details
library(simulateGP)

Attaching package: 'simulateGP'
The following objects are masked from 'package:TwoSampleMR':

    allele_frequency, contingency, get_population_allele_frequency
iv_bias <- function(g, x, y) {
    bgx = cov(g, x) / var(g)
    bgy = cov(g, y) / var(g)
    return(bgy/bgx)
}

ols_bias <- function(x, y) {
    return(cov(x,y)/var(x))
}

n <- 100000
g <- rbinom(n, 2, 0.4)
u <- g + rnorm(n, 0, sqrt(1 - var(g)))

bux <- 0.5
buy <- 0.5
y <- u * buy + rnorm(n, sd=sqrt(1-buy^2))
x <- u * bux + rnorm(n, sd=sqrt(1-bux^2))


iv_bias(g, x, y)
[1] 0.9936364
ols_bias(x,y)
[1] 0.2451663
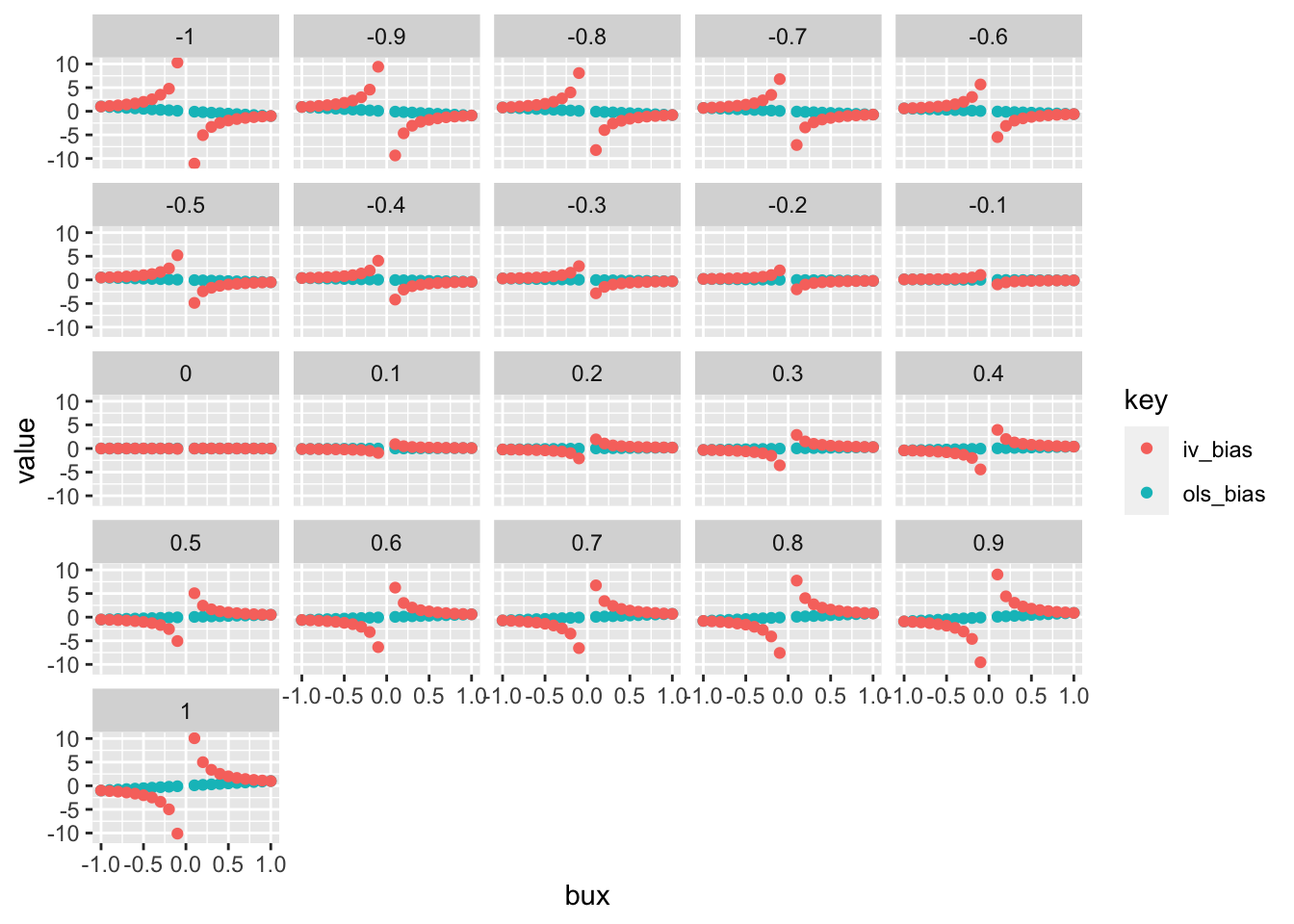
param1 <- expand.grid(
    bux=seq(-1, 1, by=0.1),
    buy=seq(-1, 1, by=0.1)
)

for(i in 1:nrow(param1)) {
    y <- u * param1$buy[i] + rnorm(n, sd=sqrt(1-param1$buy[i]^2))
    x <- u * param1$bux[i] + rnorm(n, sd=sqrt(1-param1$bux[i]^2))
    param1$ols_bias[i] <- ols_bias(x, y)
    param1$iv_bias[i] <- iv_bias(g, x, y)
    param1$ols_bias_e[i] <- param1$buy[i] * param1$bux[i]
    param1$iv_bias_e[i] <- param1$buy[i] / param1$bux[i]
}

param1 %>% filter(bux != 0) %>%
gather(key="key", value="value", c(ols_bias, iv_bias)) %>% 
ggplot(., aes(x=bux, y=value)) +
geom_point(aes(colour=key)) +
facet_wrap(~ buy)

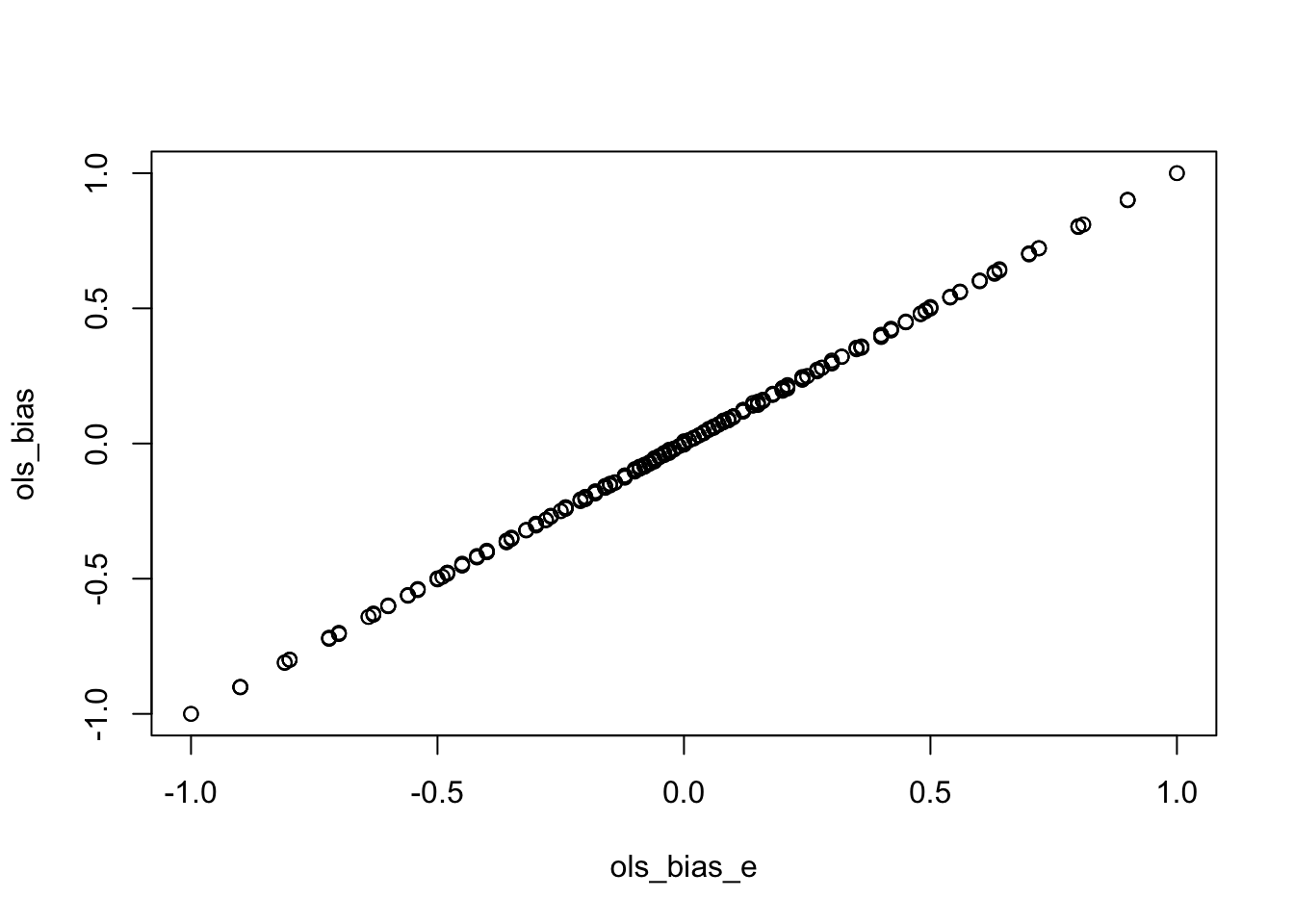
Is expected bias correct

plot(ols_bias ~ ols_bias_e, param1)

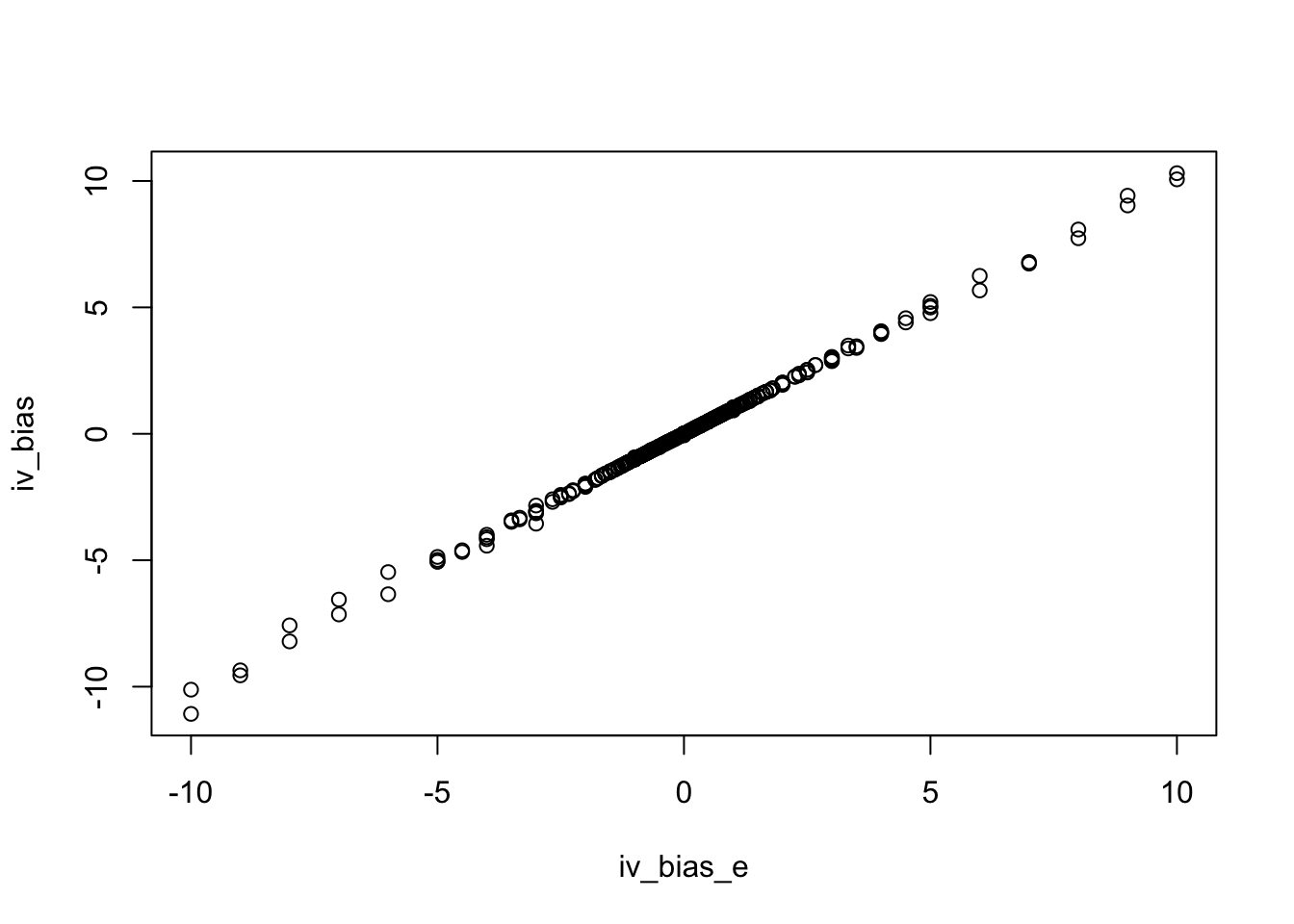
plot(iv_bias ~ iv_bias_e, param1 %>% filter(bux!=0))

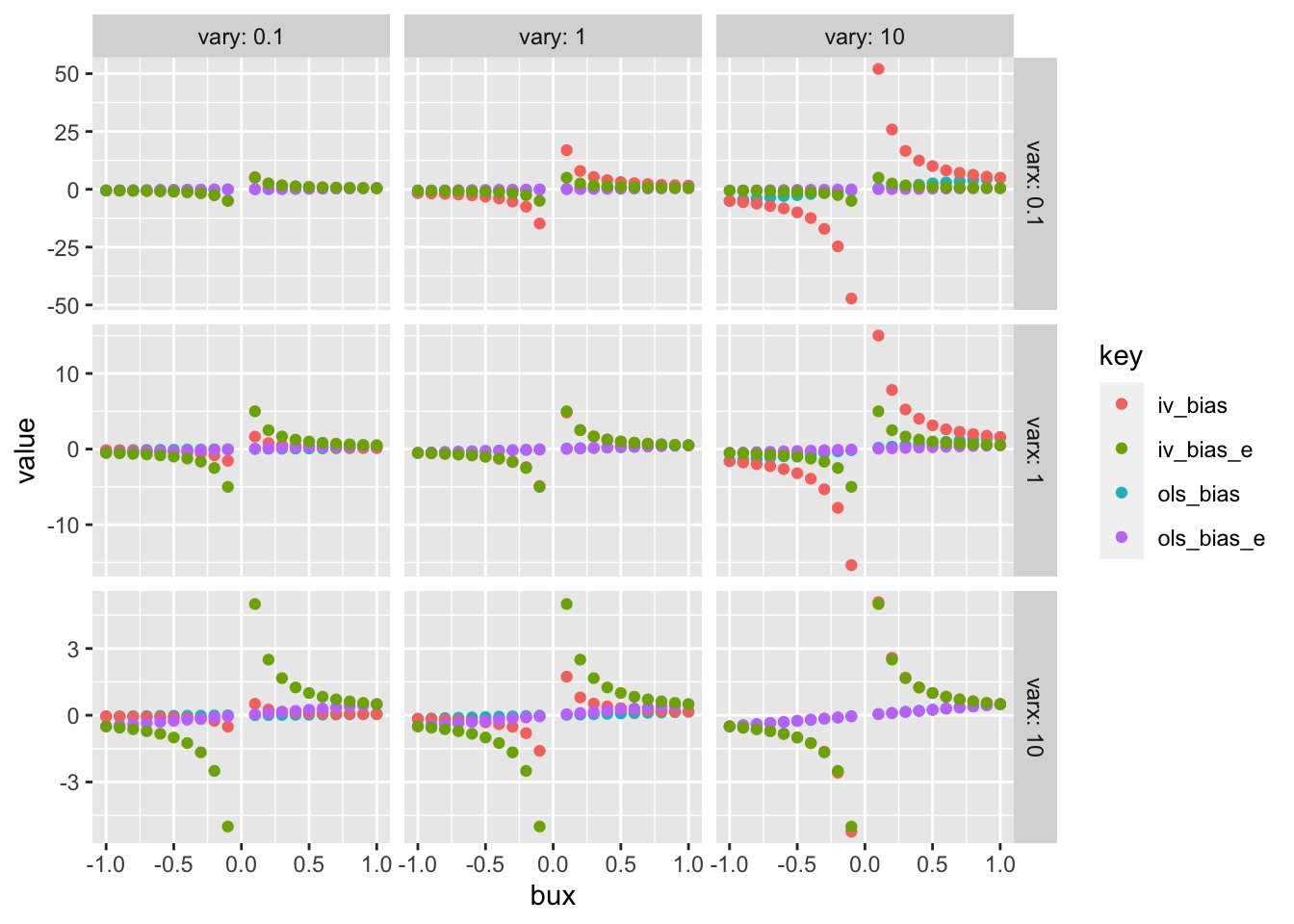
now change the variances

param2 <- expand.grid(
    bux=seq(-1, 1, by=0.1),
    buy=0.5,
    varx=c(1, 0.1, 10),
    vary=c(1, 0.1, 10)
)

for(i in 1:nrow(param2)) {
    y <- u * param2$buy[i] + rnorm(n, sd=sqrt(1-param2$buy[i]^2))
    x <- u * param2$bux[i] + rnorm(n, sd=sqrt(1-param2$bux[i]^2))
    y <- y * sqrt(param2$vary[i])
    x <- x * sqrt(param2$varx[i])
    param2$ols_bias[i] <- ols_bias(x, y)
    param2$iv_bias[i] <- iv_bias(g, x, y)
    param2$ols_bias_e[i] <- param2$buy[i] * param2$bux[i]
    param2$iv_bias_e[i] <- param2$buy[i] / param2$bux[i]
}

param2 <- param2 %>% filter(bux != 0)
param2 <- bind_rows(
    param2 %>% select(-c(ols_bias_e, iv_bias_e)) %>% gather(key="key", value="value", c(ols_bias, iv_bias)) %>% mutate(what="obs"),
    param2 %>% select(-c(ols_bias, iv_bias)) %>% gather(key="key", value="value", c(ols_bias_e, iv_bias_e)) %>% mutate(what="exp") 
)
ggplot(param2, aes(x=bux, y=value)) +
geom_point(aes(colour=key)) +
facet_grid(varx ~ vary, labeller=label_both, scale="free_y")

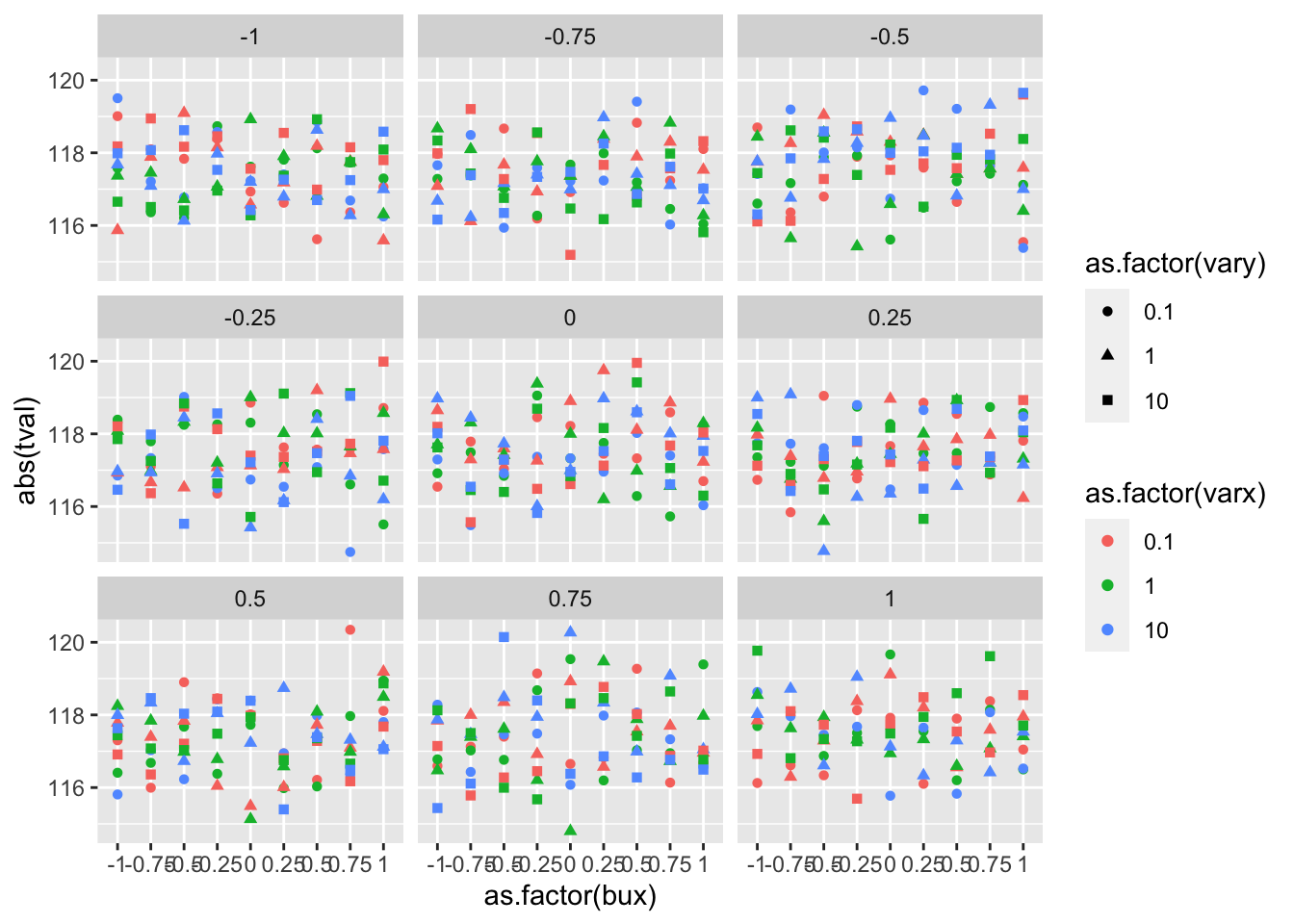
change the variance only, see if it changes test statistic

param3 <- expand.grid(
    bux=seq(-1, 1, by=0.25),
    buy=seq(-1, 1, by=0.25),
    varx=c(0.1, 1, 10),
    vary=c(0.1, 1, 10)
) %>% mutate(sim=1:n())

param3 <- lapply(1:nrow(param3), function(i) {
    y <- u * param2$buy[i] + rnorm(n, sd=sqrt(1-param2$buy[i]^2))
    x <- u * param2$bux[i] + rnorm(n, sd=sqrt(1-param2$bux[i]^2))
    y <- y * sqrt(param2$vary[i])
    x <- x * sqrt(param2$varx[i])
    get_effs(x, y, as.matrix(g)) %>% mr %>% suppressMessages %>% mutate(sim=i)
}) %>% bind_rows() %>% inner_join(., param3, by="sim")
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$buy[i]^2)): NAs produced
Warning in rnorm(n, sd = sqrt(1 - param2$bux[i]^2)): NAs produced
param3$tval <- param3$b/param3$se

param3 %>% group_by(bux, buy) %>%
    summarise(m=mean(tval), s=sd(tval))
`summarise()` has grouped output by 'bux'. You can override using the `.groups`
argument.
# A tibble: 81 × 4
# Groups:   bux [9]
     bux   buy      m       s
   <dbl> <dbl>  <dbl>   <dbl>
 1 -1    -1    -118.    1.11 
 2 -1    -0.75   91.3  78.5  
 3 -1    -0.5   -65.1 104.   
 4 -1    -0.25   39.0 118.   
 5 -1     0     -13.5 124.   
 6 -1     0.25  -12.8 124.   
 7 -1     0.5    39.1 117.   
 8 -1     0.75  -65.3 103.   
 9 -1     1     118.    1.11 
10 -0.75 -1    -118.    0.826
# ℹ 71 more rows
param3 %>% ggplot(., aes(x=as.factor(bux), y=abs(tval))) +
geom_point(aes(colour=as.factor(varx), shape=as.factor(vary))) +
facet_wrap(~ buy)

sessionInfo()
R version 4.3.0 (2023-04-21)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.6.8

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

time zone: Europe/London
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] simulateGP_0.1.2  TwoSampleMR_0.5.7 dplyr_1.1.2       tidyr_1.3.0      
[5] ggplot2_3.4.2    

loaded via a namespace (and not attached):
 [1] vctrs_0.6.2       cli_3.6.1         knitr_1.43        rlang_1.1.1      
 [5] xfun_0.39         purrr_1.0.1       generics_0.1.3    jsonlite_1.8.5   
 [9] labeling_0.4.2    glue_1.6.2        colorspace_2.1-0  plyr_1.8.8       
[13] htmltools_0.5.5   scales_1.2.1      fansi_1.0.4       rmarkdown_2.22   
[17] grid_4.3.0        evaluate_0.21     munsell_0.5.0     tibble_3.2.1     
[21] fastmap_1.1.1     yaml_2.3.7        lifecycle_1.0.3   compiler_4.3.0   
[25] Rcpp_1.0.10       htmlwidgets_1.6.2 pkgconfig_2.0.3   rstudioapi_0.14  
[29] farver_2.1.1      digest_0.6.31     R6_2.5.1          tidyselect_1.2.0 
[33] utf8_1.2.3        pillar_1.9.0      magrittr_2.0.3    withr_2.5.0      
[37] tools_4.3.0       gtable_0.3.3