Background
Data generating model
\[
y_i = \alpha + \beta_{1,j}G_{ij} + z_i + v_i + e_i
\]
where \(\alpha\) is an intercept term, \(\beta_{1,j}\) is the additive effect of SNP $j$, \(G_{i,j}\) is the genotype value for individual \(i\) at SNP $j$, \(z_i\) is the remaining polygenic risk
\[
z_i \sim N(0, \sigma^2_{g} - 2p_j(1-p_j)\beta_{1,j}^2)
\]
\(v_i\) is the SNP’s influence on dispersion where
\[
v_i \sim N(0, \beta_{2,j}G_{i,j})
\]
and \(e_i\) is the residual variance
\[
e_i \sim N(0, 1 - \sigma^2_g - \sigma^2_v)
\]
To estimate dispersion effects amongst unrelateds use the deviation regression model (DRM) from Marderstein et al 2021 AJHG (https://doi.org/10.1016/j.ajhg.2020.11.016 ).
To estimate variance heterogeneity effects using MZs, simply
\[
|y_{i,A} - y_{i,B}| = \hat{\beta}_{2,j}G_{i,j} + \epsilon_i
\]
where A and B represent the individuals in the MZ pair.
To estimate variance heterogeneity effects using siblings, it is identical to the MZ method but restricted to sibling pairs who have identity by state value of 2 (i.e. share the same genotype value at the SNP being tested).
Simulations
Attaching package: 'dplyr'
The following objects are masked from 'package:stats':
filter, lag
The following objects are masked from 'package:base':
intersect, setdiff, setequal, union
library (ggplot2)library (tidyr)library (simulateGP)
Method for simulating dispersion effects in unrelated individuals
<- function (n, beta1, beta2, af, h2)<- rbinom (n, 2 , af)<- g * beta1<- rnorm (n, 0 , h2)<- rnorm (n, 0 , beta2 * g)<- rnorm (n, 0 , sqrt (1 - var (vg) - var (v) - var (prs)))<- prs + v + vg + vereturn (tibble (<- sim_pop (100000 , 0.1 , 0.5 , 0.3 , 0.1 )var (a)
g y
g 0.42156007 0.04317622
y 0.04317622 1.00325833
Method for simulating dispersion effects in monozogytic twins
<- function (n, beta1, beta2, af, h2)<- rbinom (n, 2 , af)<- g * beta1<- rnorm (n, 0 , h2)<- rnorm (n, 0 , beta2 * g)<- rnorm (n, 0 , sqrt (1 - var (vg) - var (v1) - var (prs)))<- prs + v1 + vg + ve1<- rnorm (n, 0 , beta2 * g)<- rnorm (n, 0 , sqrt (1 - var (vg) - var (v2) - var (prs)))<- prs + v2 + vg + ve2return (tibble (<- sim_mz (100000 , 0.1 , 0.5 , 0.3 , 0.1 )var (a)
g y1 y2
g 0.42132978 0.04268190 0.04133108
y1 0.04268190 0.99914199 0.01694312
y2 0.04133108 0.01694312 1.00232809
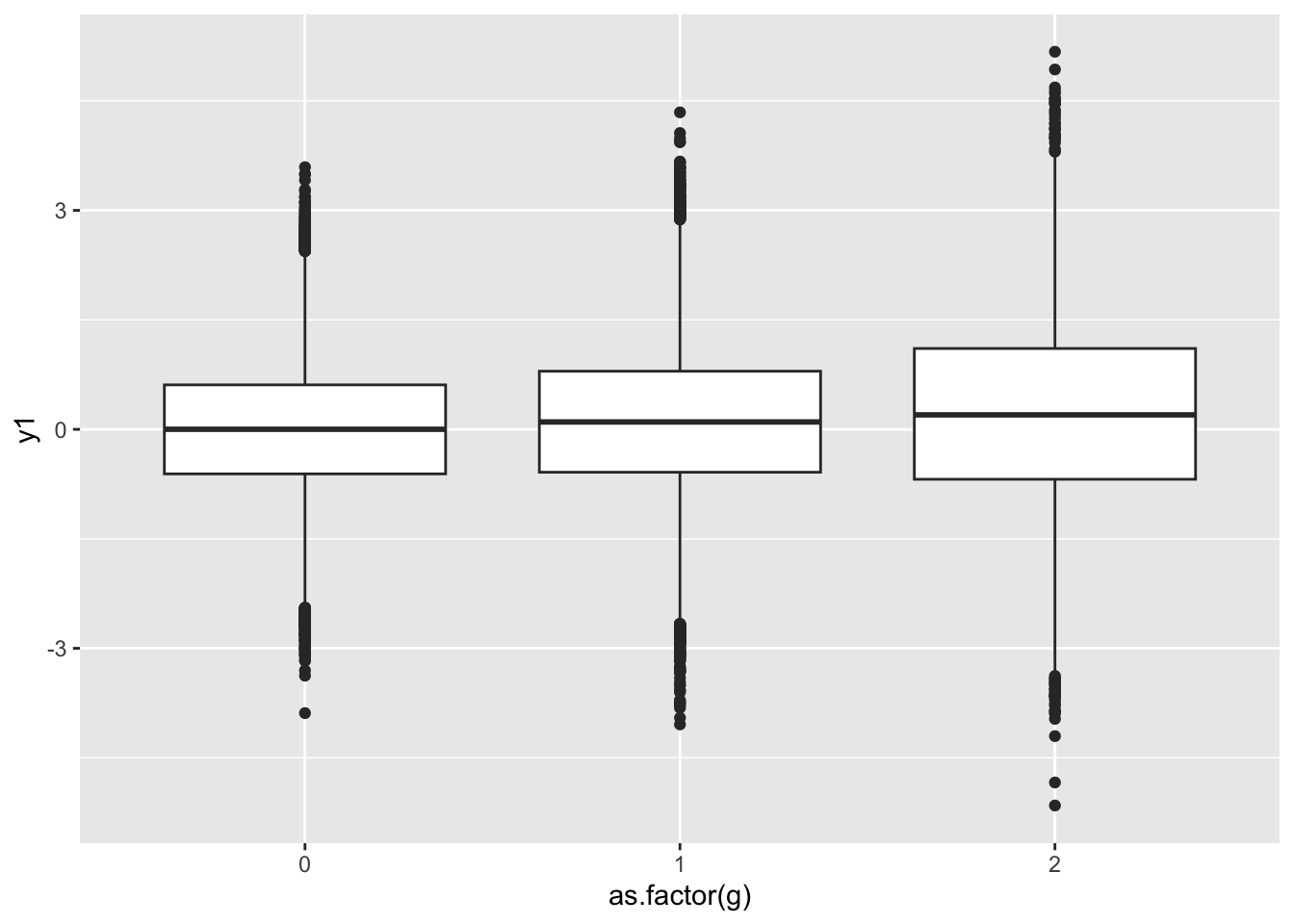
See what dispersion looks like from this simulation
%>% ggplot (., aes (x= as.factor (g), y= y1)) + geom_boxplot ()
Summarise the dispersion. Note - how would you scale it to the MZ pair mean?
<- sim_mz (100000 , 0.1 , 0.5 , 0.3 , 0.8 )%>% group_by (g) %>% summarise (m= mean (y1), v= var (y1), mzv= mean (abs (y1- y2))
# A tibble: 3 × 4
g m v mzv
<int> <dbl> <dbl> <dbl>
1 0 0.00572 0.799 0.455
2 1 0.102 1.05 0.720
3 2 0.193 1.84 1.22
Method for testing unrelateds using DRM
<- function (g, y)<- tapply (y, g, median, na.rm= T) <- abs (y - y.i[g+ 1 ])summary (lm (z.ij ~ g))$ coef %>% as_tibble () %>% slice (2 ) %>% mutate (method= "drm" )test_drm (a$ g, a$ y1)
# A tibble: 1 × 5
Estimate `Std. Error` `t value` `Pr(>|t|)` method
<dbl> <dbl> <dbl> <dbl> <chr>
1 0.154 0.00295 52.1 0 drm
Method for testing using MZs
<- function (g, y1, y2)<- abs (y1- y2)<- summary (lm (yd1 ~ g))$ coef %>% as_tibble () %>% slice (2 ) %>% mutate (method= "mzdiff" )test_mz (a$ g, a$ y1, a$ y2)
# A tibble: 1 × 5
Estimate `Std. Error` `t value` `Pr(>|t|)` method
<dbl> <dbl> <dbl> <dbl> <chr>
1 0.336 0.00250 134. 0 mzdiff
Power simulations
A trait with high heritability will have vQTL (dispersion) effects that are relatively large in MZs, but heritability shouldn’t have a major part to play in unrelateds for estimating vQTL effects.
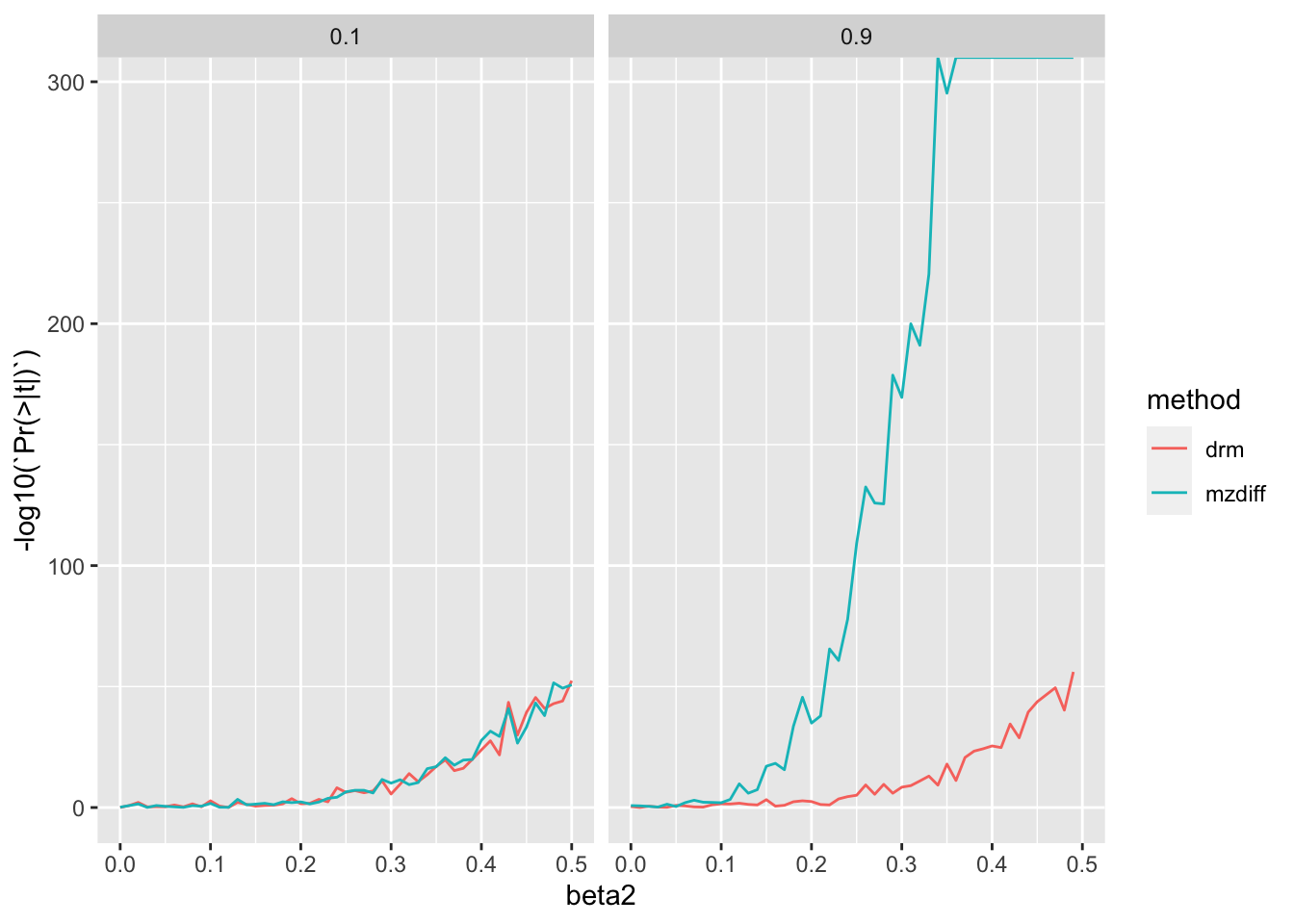
Start with simulations where population is compared against mz and n pop = n mz pairs.
<- expand.grid (beta1 = 0 ,beta2 = seq (0 , 0.5 , by= 0.01 ),h2 = c (0.1 , 0.9 ),af = 0.3 ,n = 10000 dim (param)<- lapply (1 : nrow (param), function (i)<- do.call (sim_mz, param[i,])if (any (is.na (a$ y1)) | any (is.na (a$ y2)))return (NULL )bind_rows (test_mz (a$ g, a$ y1, a$ y2),test_drm (a$ g, a$ y1)%>% bind_cols (., param[i,])%>% bind_rows ()
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
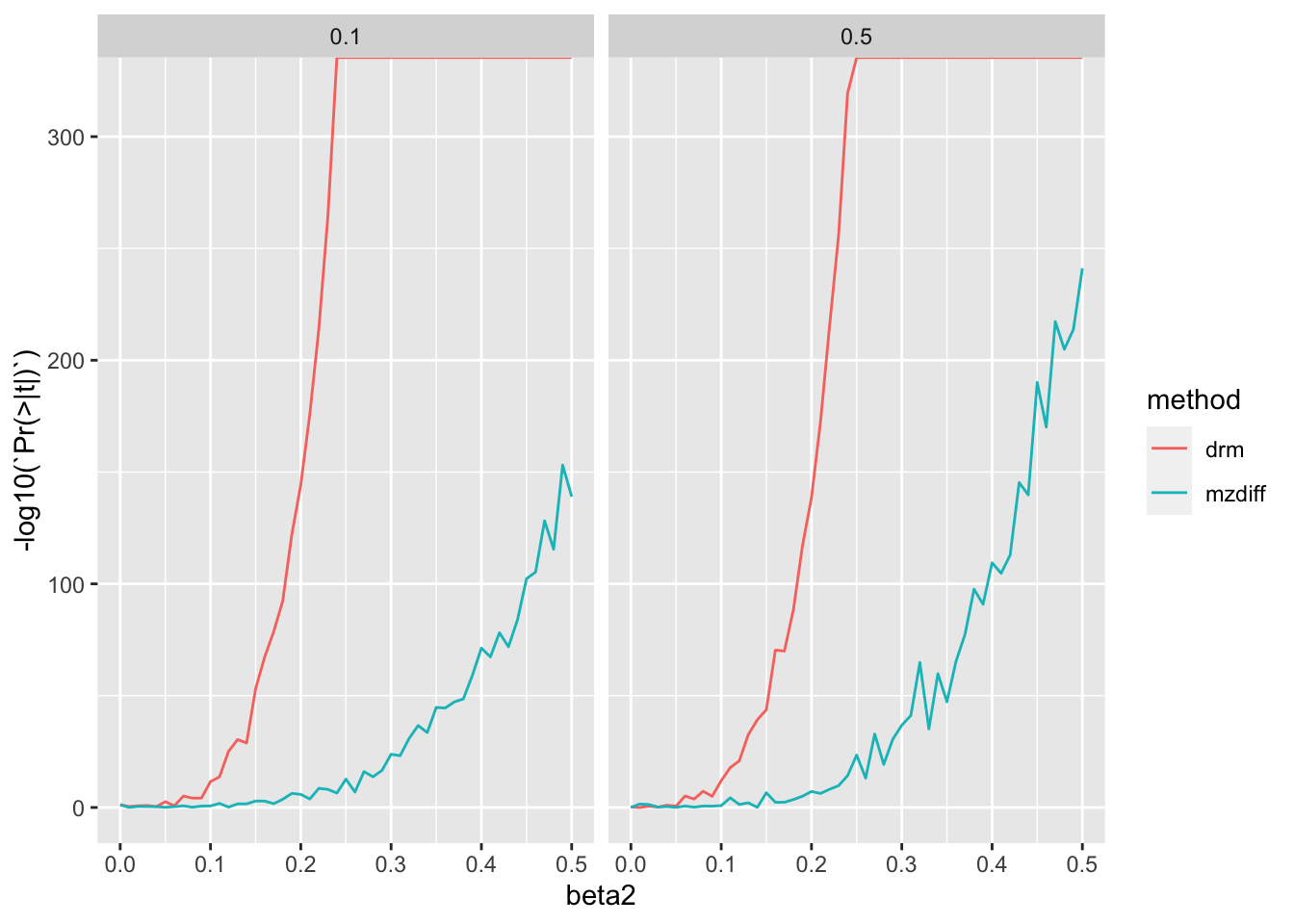
%>% filter (n== 10000 ) %>% ggplot (., aes (x= beta2, y= - log10 (` Pr(>|t|) ` ))) + geom_line (aes (colour= method)) + facet_grid (. ~ h2)
They are comparable at low heritability but as heritability increases, MZ method has a distinct advantage.
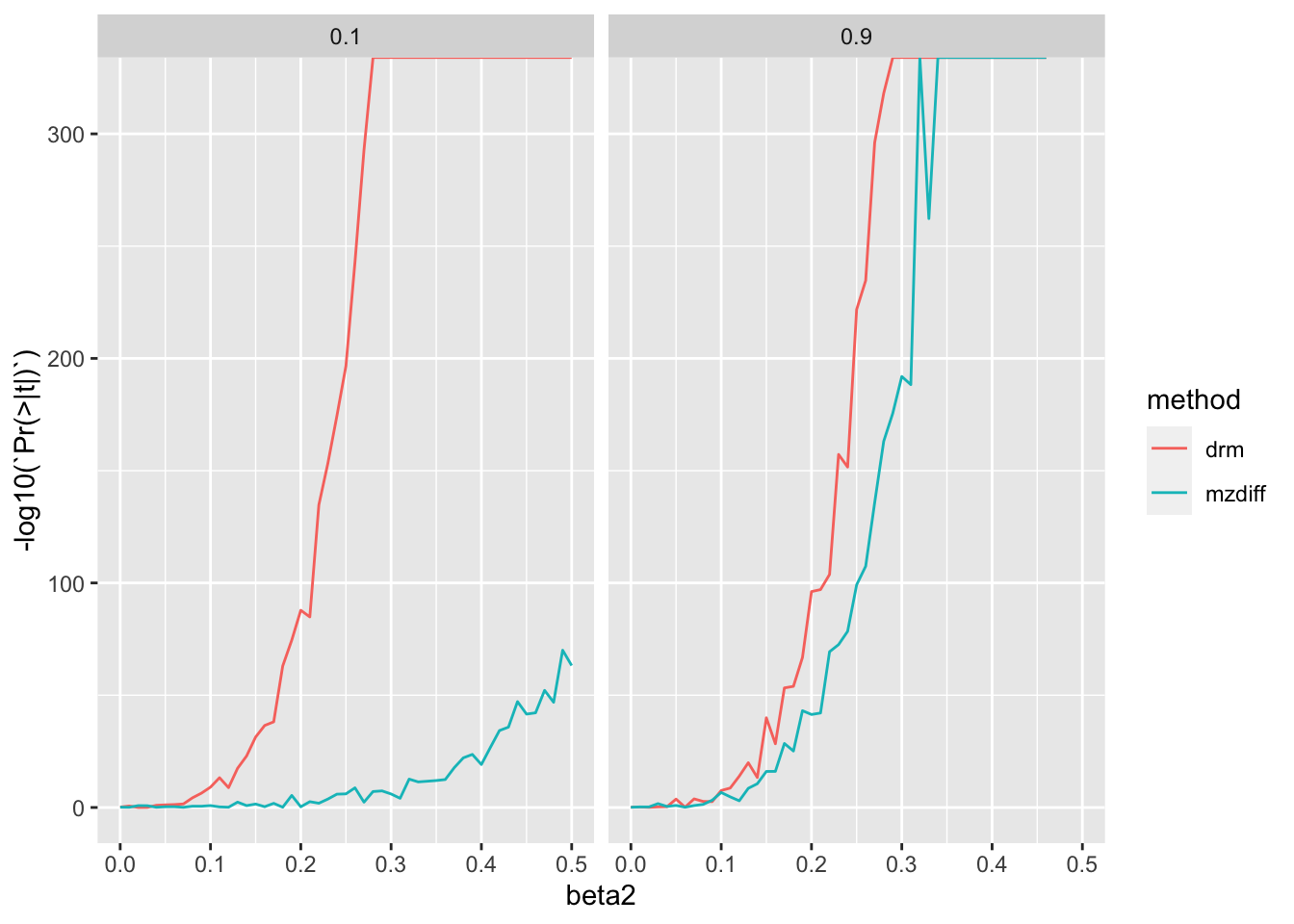
Now compare with more realistic sample sizes, 10k mz pairs vs 500k unrelateds
<- expand.grid (beta1 = 0 ,beta2 = seq (0 , 0.5 , by= 0.01 ),h2 = c (0.1 , 0.9 ),af = 0.32 dim (param)<- lapply (1 : nrow (param), function (i)<- do.call (sim_mz, param[i,] %>% mutate (n= 10000 ))<- do.call (sim_mz, param[i,] %>% mutate (n= 500000 ))if (any (is.na (a1$ y1)) | any (is.na (a1$ y2)) | any (is.na (a2$ y1)) | any (is.na (a2$ y2)))return (NULL )bind_rows (test_mz (a1$ g, a1$ y1, a1$ y2),test_drm (a2$ g, a2$ y1)%>% bind_cols (., param[i,])%>% bind_rows ()
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v1) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v1) - var(prs))): NAs produced
Warning in sqrt(1 - var(vg) - var(v2) - var(prs)): NaNs produced
Warning in rnorm(n, 0, sqrt(1 - var(vg) - var(v2) - var(prs))): NAs produced
ggplot (res2, aes (x= beta2, y= - log10 (` Pr(>|t|) ` ))) + geom_line (aes (colour= method)) + facet_grid (. ~ h2)
It looks like you’d just be better off with estimation in populations.
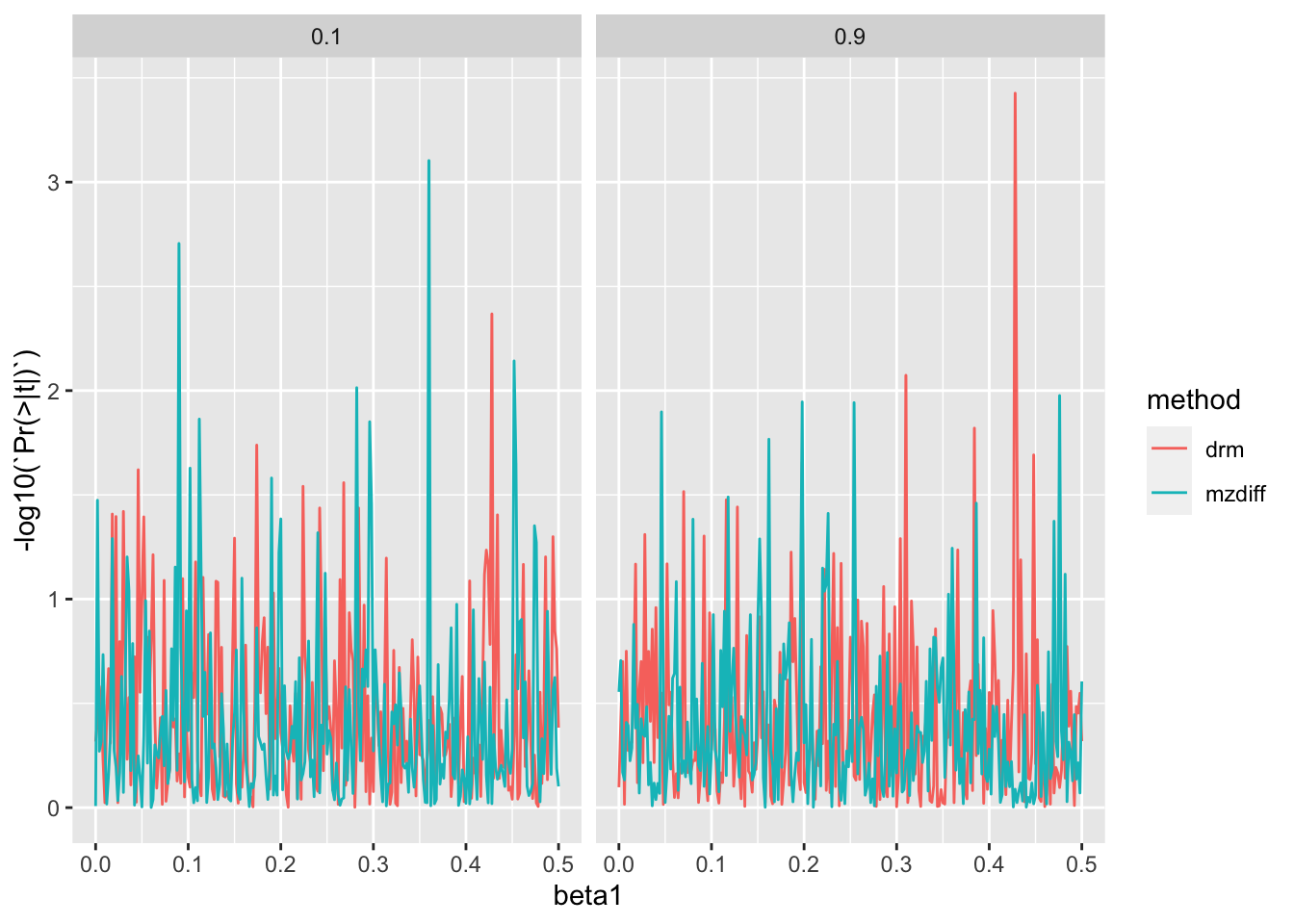
Type 1 error
<- expand.grid (beta1 = seq (0 , 0.5 , by= 0.002 ),beta2 = 0 ,h2 = c (0.1 , 0.9 ),af = 0.32 dim (param)<- lapply (1 : nrow (param), function (i)<- do.call (sim_mz, param[i,] %>% mutate (n= 10000 ))<- do.call (sim_mz, param[i,] %>% mutate (n= 500000 ))if (any (is.na (a1$ y1)) | any (is.na (a1$ y2)) | any (is.na (a2$ y1)) | any (is.na (a2$ y2)))return (NULL )bind_rows (test_mz (a1$ g, a1$ y1, a1$ y2),test_drm (a2$ g, a2$ y1)%>% bind_cols (., param[i,])%>% bind_rows ()
Plot type 1 error
ggplot (res3, aes (x= beta1, y= - log10 (` Pr(>|t|) ` ))) + geom_line (aes (colour= method)) + facet_grid (. ~ h2)
Type 1 error and number of false positives after multiple testing correction
%>% mutate (fdr= p.adjust (` Pr(>|t|) ` , "fdr" )) %>% group_by (method, h2) %>% summarise (t1 = sum (` Pr(>|t|) ` < 0.05 , na.rm= T)/ sum (! is.na (` Pr(>|t|) ` )),nfdr = sum (fdr < 0.05 )/ sum (! is.na (` Pr(>|t|) ` ))
`summarise()` has grouped output by 'method'. You can override using the
`.groups` argument.
# A tibble: 4 × 4
# Groups: method [2]
method h2 t1 nfdr
<chr> <dbl> <dbl> <dbl>
1 drm 0.1 0.0478 0
2 drm 0.9 0.0438 0
3 mzdiff 0.1 0.0558 0
4 mzdiff 0.9 0.0398 0
Under normal distribution type-1 error rate is well controlled.
Simulations using siblings
Generate a set of sib pairs with the following specification
Have PRS such that IBD ~ N(0.5, sqrt(0.037))
h2 specified
ce specified (shared variance between sibs
one SNP has a mean and variance effect
scaled phenotypes ~ N(0, 1)
<- function (af, nfam, beta1, beta2, h2, c2)# Choose number of SNPs to be expected number of recombination events # in order to give appropriate distribution of IBD <- 87 <- rep (af, nsnp)<- matrix (0 , nfam, nsnp)<- matrix (0 , nfam, nsnp)<- matrix (0 , nfam, nsnp)<- matrix (0 , nfam, nsnp)<- matrix (0 , nfam, nsnp)<- matrix (0 , nfam, nsnp)for (i in 1 : nsnp)<- rbinom (nfam, 1 , af[i]) + 1 <- (rbinom (nfam, 1 , af[i]) + 1 ) * - 1 <- rbinom (nfam, 1 , af[i]) + 1 <- (rbinom (nfam, 1 , af[i]) + 1 ) * - 1 <- sample (c (TRUE , FALSE ), nfam, replace= TRUE )<- rep (NA , nfam)<- dad1[dadindex]! dadindex] <- dad2[! dadindex]<- sample (c (TRUE , FALSE ), nfam, replace= TRUE )<- rep (NA , nfam)<- mum1[mumindex]! mumindex] <- mum2[! mumindex]<- cbind (dadh, mumh)<- sample (c (TRUE , FALSE ), nfam, replace= TRUE )<- rep (NA , nfam)<- dad1[dadindex]! dadindex] <- dad2[! dadindex]<- sample (c (TRUE , FALSE ), nfam, replace= TRUE )<- rep (NA , nfam)<- mum1[mumindex]! mumindex] <- mum2[! mumindex]<- cbind (dadh, mumh)<- (as.numeric (sib1[,1 ] == sib2[,1 ]) + as.numeric (sib1[,2 ] == sib2[,2 ])) / 2 <- rowSums (abs (sib1) - 1 )<- rowSums (abs (sib2) - 1 )<- dad1 - 1 + abs (dad2) - 1 <- mum1 - 1 + abs (mum2) - 1 # l[[i]] <- (sum(sib1[,1] == sib2[,1]) / nsnp + sum(sib1[,2] == sib2[,2]) / nsnp) / 2 <- nfam# Make phenotypes <- rnorm (n, 0 , sqrt (c2))<- rnorm (n, 0 , beta2 * sibs1[,1 ])<- rnorm (n, 0 , beta2 * sibs2[,1 ])<- rnorm (n, 0 , sqrt (1 - h2 - c2 - var (v1)))<- rnorm (n, 0 , sqrt (1 - h2 - c2 - var (v2)))<- rnorm (nsnp-1 , 0 , 1 )<- beta1^ 2 * af[1 ] * (1 - af[1 ]) * 2 <- h2 - h2_1<- scale (sibs1[,- 1 ] %*% b) * sqrt (h2_res)<- scale (sibs2[,- 1 ] %*% b) * sqrt (h2_res)<- sibs1[,1 ] * beta1 + prs1 + v1 + ce + e1<- sibs2[,1 ] * beta1 + prs2 + v2 + ce + e2return (tibble (ibd = rowMeans (ibd),g1 = sibs1[,1 ],g2 = sibs2[,1 ],
Notes
In this model if the allele frequency is higher, then the genotype class with the larger variance is more common, which means that effect alleles are not reflexive in terms of variances
I think this use with siblings may have problems due to LD. If there is incomplete LD with another causal variant elsewhere close by then the mean effect of that causal variant will contribute to the variance effect estimated at the variant
<- sim_sibs (0.3 , 10000 , 0.1 , 0.4 , 0.6 , 0.1 )cor (fam) %>% round (4 )
ibd g1 g2 prs1 prs2 y1 y2
ibd 1.0000 -0.0032 -0.0183 -0.0068 0.0024 -0.0020 0.0062
g1 -0.0032 1.0000 0.4970 0.0130 0.0195 0.0704 0.0395
g2 -0.0183 0.4970 1.0000 0.0074 0.0160 0.0434 0.0750
prs1 -0.0068 0.0130 0.0074 1.0000 0.5023 0.7720 0.3840
prs2 0.0024 0.0195 0.0160 0.5023 1.0000 0.4043 0.7777
y1 -0.0020 0.0704 0.0434 0.7720 0.4043 1.0000 0.4139
y2 0.0062 0.0395 0.0750 0.3840 0.7777 0.4139 1.0000
Now how to estimate variance effect? At a locus restrict to sib pairs who are IBD = 1
<- sim_sibs (af= 0.5 , nfam= 40000 , beta1= 0.1 , beta2= 0.2 , h2= 0.3 , c2= 0.1 )
# A tibble: 40,000 × 7
ibd g1 g2 prs1[,1] prs2[,1] y1[,1] y2[,1]
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.477 0 2 0.542 0.307 0.958 -0.0552
2 0.552 1 1 0.0251 -0.459 0.888 -0.675
3 0.5 1 1 -0.254 -0.164 -1.38 -0.596
4 0.517 1 0 0.252 -0.522 1.72 -0.171
5 0.517 1 1 -0.197 -0.183 0.343 -1.36
6 0.534 1 1 0.838 0.526 1.03 1.16
7 0.483 0 0 0.383 -0.524 -0.974 -0.727
8 0.5 2 1 -0.291 -0.291 0.0133 -0.884
9 0.534 1 1 0.310 -0.627 0.362 -0.852
10 0.494 0 0 0.576 0.0136 1.06 -1.01
# … with 39,990 more rows
Test for variance QTL
<- sim_sibs (af= 0.5 , nfam= 40000 , beta1= 0.1 , beta2= 0.2 , h2= 0.01 , c2= 0.01 )<- subset (fam, g1== g2)test_mz (f1$ g1, f1$ y1, f1$ y2)
# A tibble: 1 × 5
Estimate `Std. Error` `t value` `Pr(>|t|)` method
<dbl> <dbl> <dbl> <dbl> <chr>
1 0.0438 0.00798 5.50 0.0000000394 mzdiff
Power sims
<- expand.grid (beta1 = 0 ,beta2 = seq (0 , 0.5 , by= 0.01 ),c2 = c (0 ),h2 = c (0.1 , 0.5 ),af = c (0.5 )dim (param)<- lapply (1 : nrow (param), function (i)<- do.call (sim_sibs, param[i,] %>% mutate (nfam= 22000 ))<- do.call (sim_pop, param[i,] %>% select (- c (c2)) %>% mutate (n= 500000 ))if (any (is.na (a1$ y1)) | any (is.na (a1$ y2)) | any (is.na (a2$ y)))return (NULL )bind_rows (%>% filter (g1== g2) %>% select (g= g1, y1, y2) %>% do.call (test_mz, .),do.call (test_drm, a2)%>% bind_cols (., param[i,])%>% bind_rows ()
%>% mutate (sharing= c2+ h2) %>% filter (beta1== 0 ) %>% ggplot (., aes (x= beta2, y= - log10 (` Pr(>|t|) ` ))) + geom_line (aes (colour= method, groups= af)) + facet_grid (. ~ sharing)
Warning in geom_line(aes(colour = method, groups = af)): Ignoring unknown
aesthetics: groups
Similar to MZ method - quite a substantial benefit from leveraging large sample sizes of unrelateds compared to using siblings.
SVLM
Adjust the phenotype for covariates + genotype, square residuals and then test in linear model against genotype.
<- function (g, y)<- residuals (lm (y ~ g))^ 2 summary (lm (yres ~ g))$ coefficients %>% as_tibble () %>% slice (n= 2 ) %>% mutate (method= "svlm" )
<- 10000 <- rbinom (n, 2 , 0.4 )<- rbinom (n, 2 , 0.4 )<- g1 + g2 + g1 * g2bind_rows (test_drm (g1, y),test_svlm (g1, y)
# A tibble: 2 × 5
Estimate `Std. Error` `t value` `Pr(>|t|)` method
<dbl> <dbl> <dbl> <dbl> <chr>
1 0.524 0.0139 37.7 2.06e-291 drm
2 1.85 0.0333 55.7 0 svlm
<- g1 + g2 + rnorm (n)bind_rows (test_drm (g1, y),test_svlm (g1, y)
# A tibble: 2 × 5
Estimate `Std. Error` `t value` `Pr(>|t|)` method
<dbl> <dbl> <dbl> <dbl> <chr>
1 0.000577 0.0104 0.0557 0.956 drm
2 0.00402 0.0286 0.141 0.888 svlm
<- g1 + g2 + g1 * g2<- residuals (lm (y ~ g1 + g2))^ 2 summary (lm (yres ~ g1))
Call:
lm(formula = yres ~ g1)
Residuals:
Min 1Q Median 3Q Max
-0.2912 -0.2516 -0.1973 0.2402 1.7333
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.155064 0.006387 24.28 <2e-16 ***
g1 0.097849 0.006041 16.20 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4188 on 9998 degrees of freedom
Multiple R-squared: 0.02557, Adjusted R-squared: 0.02547
F-statistic: 262.4 on 1 and 9998 DF, p-value: < 2.2e-16
<- residuals (lm (y ~ g1))^ 2 summary (lm (yres ~ g1))
Call:
lm(formula = yres ~ g1)
Residuals:
Min 1Q Median 3Q Max
-3.6900 -2.0229 0.2948 0.3860 8.8235
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.32939 0.03516 9.368 <2e-16 ***
g1 1.85174 0.03325 55.686 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.305 on 9998 degrees of freedom
Multiple R-squared: 0.2367, Adjusted R-squared: 0.2367
F-statistic: 3101 on 1 and 9998 DF, p-value: < 2.2e-16
Inflation due to LD
<- sapply (1 : 1000 , function (i){<- correlated_binomial (n, 0.5 , 0.5 , 0.8 )<- rbinom (n, 2 , 0.5 )<- g[,1 ] + rnorm (n)summary (lm (y ~ g[,2 ]* g2))$ coef[4 ,4 ] hist (res)
<- function (n, p1, p2, p3, r1)# dat <- simulateGP:::simulate_geno(n, r1, p1, p2) %>% as_tibble <- correlated_binomial (n, p1, p2, r1) %>% as_tibble ()names (dat) <- c ("y1" , "y2" )$ y3 <- rbinom (n, 1 , p3)return (dat)<- function (param, i)set.seed (i* 10 )<- gendatp (param$ n[i], param$ p1[i], param$ p2[i], param$ p3[i], param$ r1[i])<- dat$ y1 + rnorm (nrow (dat), sd= sd (dat$ y1)/ 2 )<- lm (x ~ y2 + y3, dat)<- lm (x ~ y2 + y3 + y2* y3, dat)<- anova (mod1, mod2)$ F[i] <- amod$ F[2 ]<- test_drm (dat$ y1, x)<- test_drm (dat$ y2, x)<- test_drm (dat$ y3, x)$ drm1[i] <- o1$ ` Pr(>|t|) ` $ drm2[i] <- o2$ ` Pr(>|t|) ` $ drm3[i] <- o3$ ` Pr(>|t|) ` return (param[i,])<- expand.grid (p1= 0.1 ,p2= 0.1 ,p3= 0.5 ,p4= 0.1 ,n= 1000 ,r1= seq (0 , 1 , by= 0.2 ),sim= 1 : 100 ,r2= NA ,F= NA ,drm1= NA ,drm2= NA ,drm3= NA <- lapply (1 : nrow (param), function (x) run_simp (param, x)) %>% bind_rows ()str (resp)
'data.frame': 600 obs. of 12 variables:
$ p1 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ p2 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ p3 : num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
$ p4 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ n : num 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 ...
$ r1 : num 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 ...
$ sim : int 1 1 1 1 1 1 2 2 2 2 ...
$ r2 : logi NA NA NA NA NA NA ...
$ F : num 0.548 2.737 2.562 0.187 2.62 ...
$ drm1: num 0.288 0.376 0.16 0.215 0.998 ...
$ drm2: num 3.24e-02 1.39e-15 8.30e-18 1.03e-20 2.35e-14 ...
$ drm3: num 0.9173 0.1256 0.0146 0.1303 0.6663 ...
- attr(*, "out.attrs")=List of 2
..$ dim : Named int [1:12] 1 1 1 1 1 6 100 1 1 1 ...
.. ..- attr(*, "names")= chr [1:12] "p1" "p2" "p3" "p4" ...
..$ dimnames:List of 12
.. ..$ p1 : chr "p1=0.1"
.. ..$ p2 : chr "p2=0.1"
.. ..$ p3 : chr "p3=0.5"
.. ..$ p4 : chr "p4=0.1"
.. ..$ n : chr "n=1000"
.. ..$ r1 : chr [1:6] "r1=0.0" "r1=0.2" "r1=0.4" "r1=0.6" ...
.. ..$ sim : chr [1:100] "sim= 1" "sim= 2" "sim= 3" "sim= 4" ...
.. ..$ r2 : chr "r2=NA"
.. ..$ F : chr "F=NA"
.. ..$ drm1: chr "drm1=NA"
.. ..$ drm2: chr "drm2=NA"
.. ..$ drm3: chr "drm3=NA"
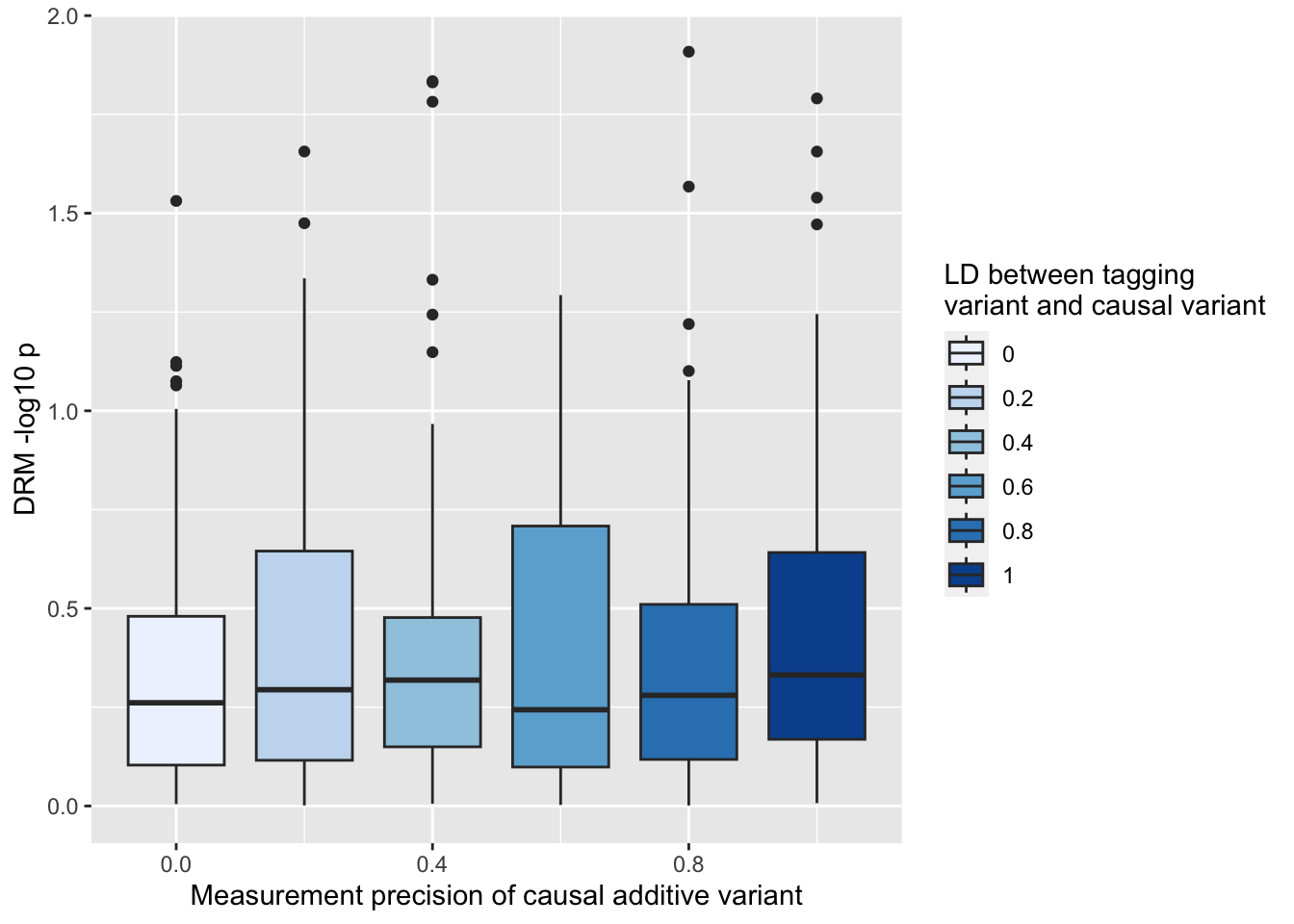
Result using the actual causal variant
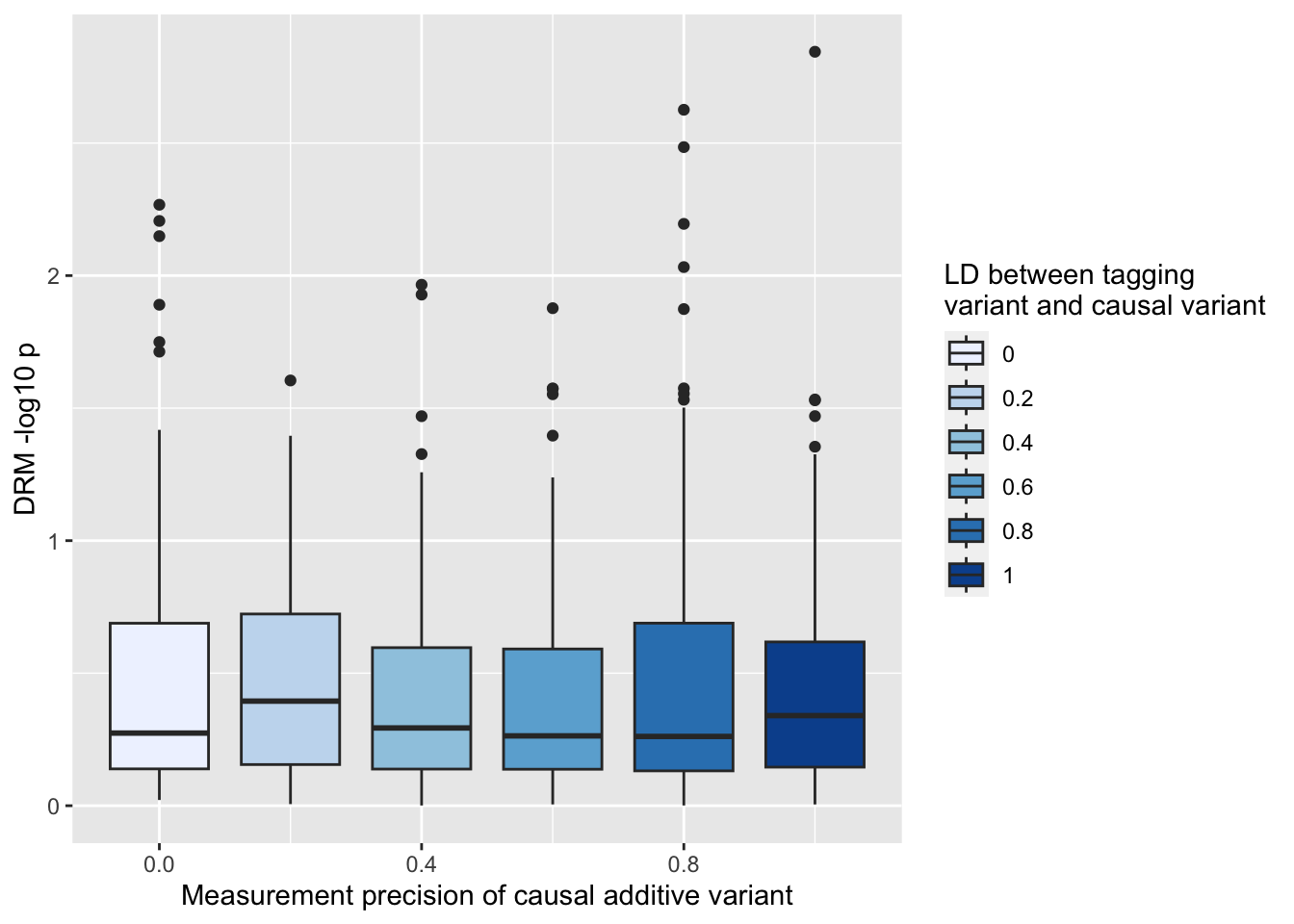
ggplot (resp, aes (x= r1, y= - log10 (drm1))) + geom_boxplot (aes (fill= as.factor (r1))) + scale_fill_brewer (type= "seq" ) + labs (y= "DRM -log10 p" , x= "Measurement precision of causal additive variant" , fill= "LD between tagging \n variant and causal variant" )
Result using
ggplot (resp, aes (x= r1, y= - log10 (drm2))) + geom_boxplot (aes (fill= as.factor (r1))) + scale_fill_brewer (type= "seq" ) + labs (y= "DRM -log10 p" , x= "Measurement precision of causal additive variant" , fill= "LD between tagging \n variant and causal variant" )
ggplot (resp, aes (x= r1, y= - log10 (drm3))) + geom_boxplot (aes (fill= as.factor (r1))) + scale_fill_brewer (type= "seq" ) + labs (y= "DRM -log10 p" , x= "Measurement precision of causal additive variant" , fill= "LD between tagging \n variant and causal variant" )
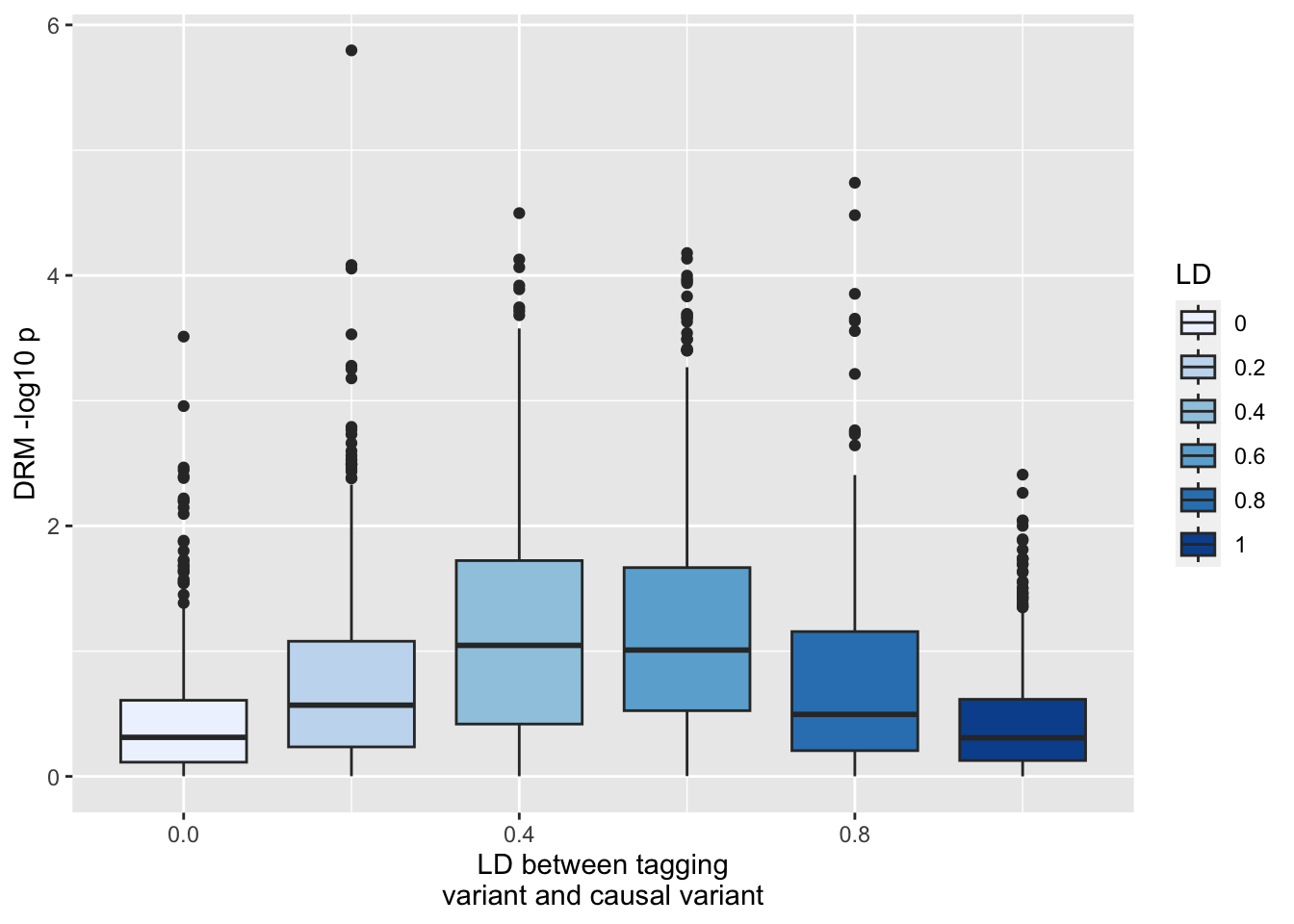
LD issue persists with MZ analysis?
<- function (g, beta1, beta2, h2)<- length (g)<- g * beta1<- rnorm (n, 0 , h2)<- rnorm (n, 0 , beta2 * g)<- rnorm (n, 0 , sqrt (1 - var (vg) - var (v1) - var (prs)))<- prs + v1 + vg + ve1<- rnorm (n, 0 , beta2 * g)<- rnorm (n, 0 , sqrt (1 - var (vg) - var (v2) - var (prs)))<- prs + v2 + vg + ve2return (tibble (<- function (g, y1, y2)<- abs (y1- y2)<- summary (lm (yd1 ~ g))$ coef %>% as_tibble () %>% slice (2 ) %>% mutate (method= "mzdiff" )<- function (n, p1, p2, p3, r1)# dat <- simulateGP:::simulate_geno(n, r1, p1, p2) %>% as_tibble <- correlated_binomial (n, p1, p2, r1) %>% as_tibble ()names (dat) <- c ("g1" , "g2" )$ g3 <- rbinom (n, 1 , p3)return (dat)<- function (param, i)set.seed (i* 10 )<- gendatp (param$ n[i], param$ p1[i], param$ p2[i], param$ p3[i], param$ r1[i])<- sim_mz2 (dat$ g1, param$ beta1[i], param$ beta2[i], param$ h2)#x <- dat$y1 + rnorm(nrow(dat), sd=sd(dat$y1)/2) <- test_drm (dat$ g1, mzdat$ y1)<- test_drm (dat$ g2, mzdat$ y1)<- test_drm (dat$ g3, mzdat$ y1)<- test_mz (dat$ g1, mzdat$ y1, mzdat$ y2)<- test_mz (dat$ g2, mzdat$ y1, mzdat$ y2)<- test_mz (dat$ g3, mzdat$ y1, mzdat$ y2)$ drm1[i] <- o1$ ` Pr(>|t|) ` $ drm2[i] <- o2$ ` Pr(>|t|) ` $ drm3[i] <- o3$ ` Pr(>|t|) ` $ mz1[i] <- m1$ ` Pr(>|t|) ` $ mz2[i] <- m2$ ` Pr(>|t|) ` $ mz3[i] <- m3$ ` Pr(>|t|) ` return (param[i,])<- expand.grid (p1= 0.1 ,p2= 0.1 ,p3= 0.5 ,p4= 0.1 ,n= 1000 ,r1= seq (0 , 1 , by= 0.2 ),beta1= 1 ,beta2= 0 ,h2= 0.5 ,sim= 1 : 500 ,r2= NA ,F= NA ,drm1= NA ,drm2= NA ,drm3= NA ,mz1= NA ,mz2= NA ,mz3= NA <- lapply (1 : nrow (param), function (i) run_simp_mz (param, i)) %>% bind_rows ()%>% str
'data.frame': 3000 obs. of 18 variables:
$ p1 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ p2 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ p3 : num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
$ p4 : num 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ...
$ n : num 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 ...
$ r1 : num 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 ...
$ beta1: num 1 1 1 1 1 1 1 1 1 1 ...
$ beta2: num 0 0 0 0 0 0 0 0 0 0 ...
$ h2 : num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
$ sim : int 1 1 1 1 1 1 2 2 2 2 ...
$ r2 : logi NA NA NA NA NA NA ...
$ F : logi NA NA NA NA NA NA ...
$ drm1 : num 0.717 0.117 0.951 0.239 0.899 ...
$ drm2 : num 0.381 0.134 0.584 0.55 0.456 ...
$ drm3 : num 0.587 0.158 0.228 0.775 0.928 ...
$ mz1 : num 0.3104 0.0677 0.9304 0.1766 0.1589 ...
$ mz2 : num 0.5393 0.2663 0.1479 0.0585 0.7089 ...
$ mz3 : num 0.483 0.977 0.943 0.169 0.369 ...
- attr(*, "out.attrs")=List of 2
..$ dim : Named int [1:18] 1 1 1 1 1 6 1 1 1 500 ...
.. ..- attr(*, "names")= chr [1:18] "p1" "p2" "p3" "p4" ...
..$ dimnames:List of 18
.. ..$ p1 : chr "p1=0.1"
.. ..$ p2 : chr "p2=0.1"
.. ..$ p3 : chr "p3=0.5"
.. ..$ p4 : chr "p4=0.1"
.. ..$ n : chr "n=1000"
.. ..$ r1 : chr [1:6] "r1=0.0" "r1=0.2" "r1=0.4" "r1=0.6" ...
.. ..$ beta1: chr "beta1=1"
.. ..$ beta2: chr "beta2=0"
.. ..$ h2 : chr "h2=0.5"
.. ..$ sim : chr [1:500] "sim= 1" "sim= 2" "sim= 3" "sim= 4" ...
.. ..$ r2 : chr "r2=NA"
.. ..$ F : chr "F=NA"
.. ..$ drm1 : chr "drm1=NA"
.. ..$ drm2 : chr "drm2=NA"
.. ..$ drm3 : chr "drm3=NA"
.. ..$ mz1 : chr "mz1=NA"
.. ..$ mz2 : chr "mz2=NA"
.. ..$ mz3 : chr "mz3=NA"
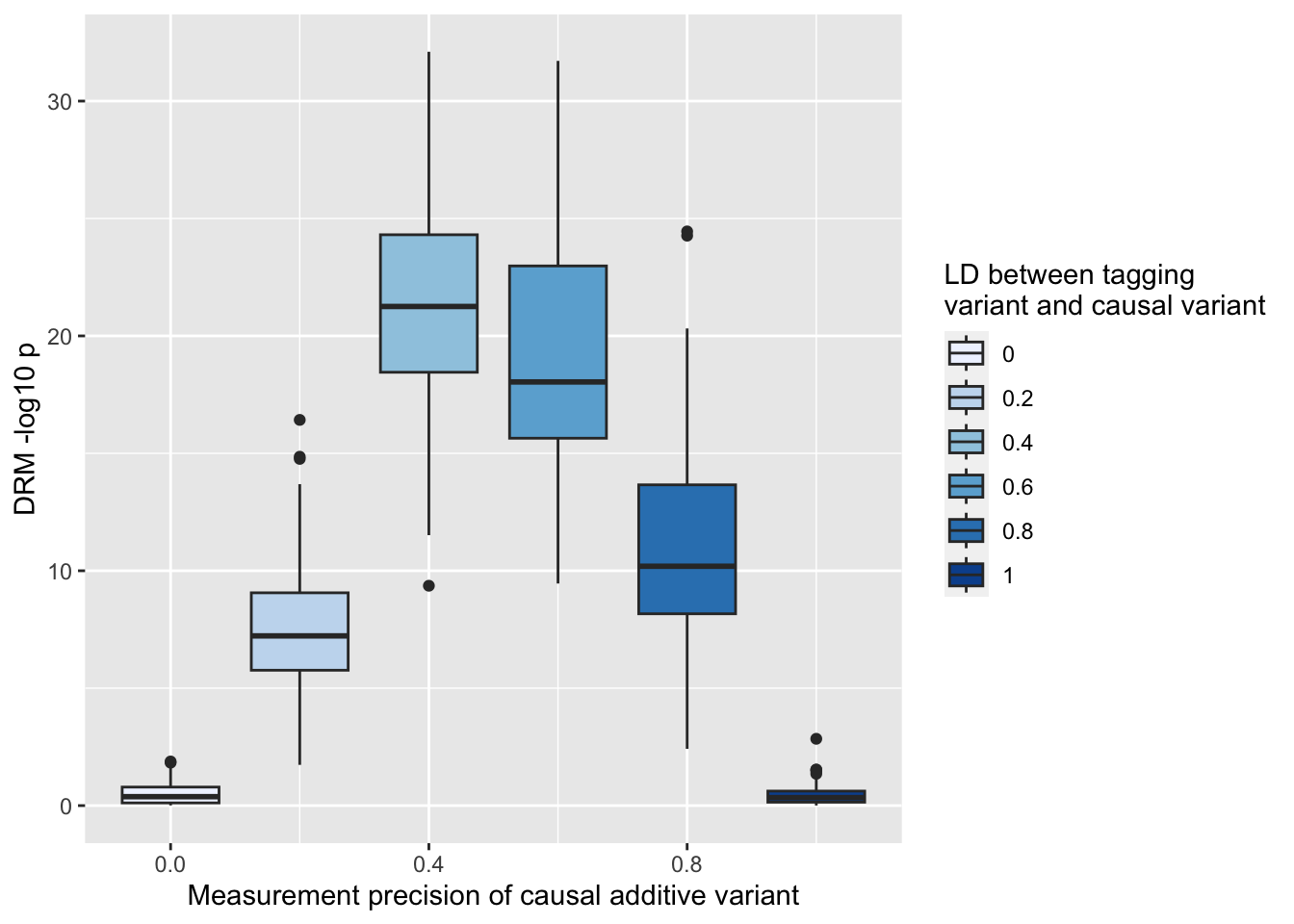
ggplot (resmz, aes (x= r1, y= - log10 (drm2))) + geom_boxplot (aes (fill= as.factor (r1))) + scale_fill_brewer (type= "seq" ) + labs (y= "DRM -log10 p" , x= "LD between tagging \n variant and causal variant" , fill= "LD" )
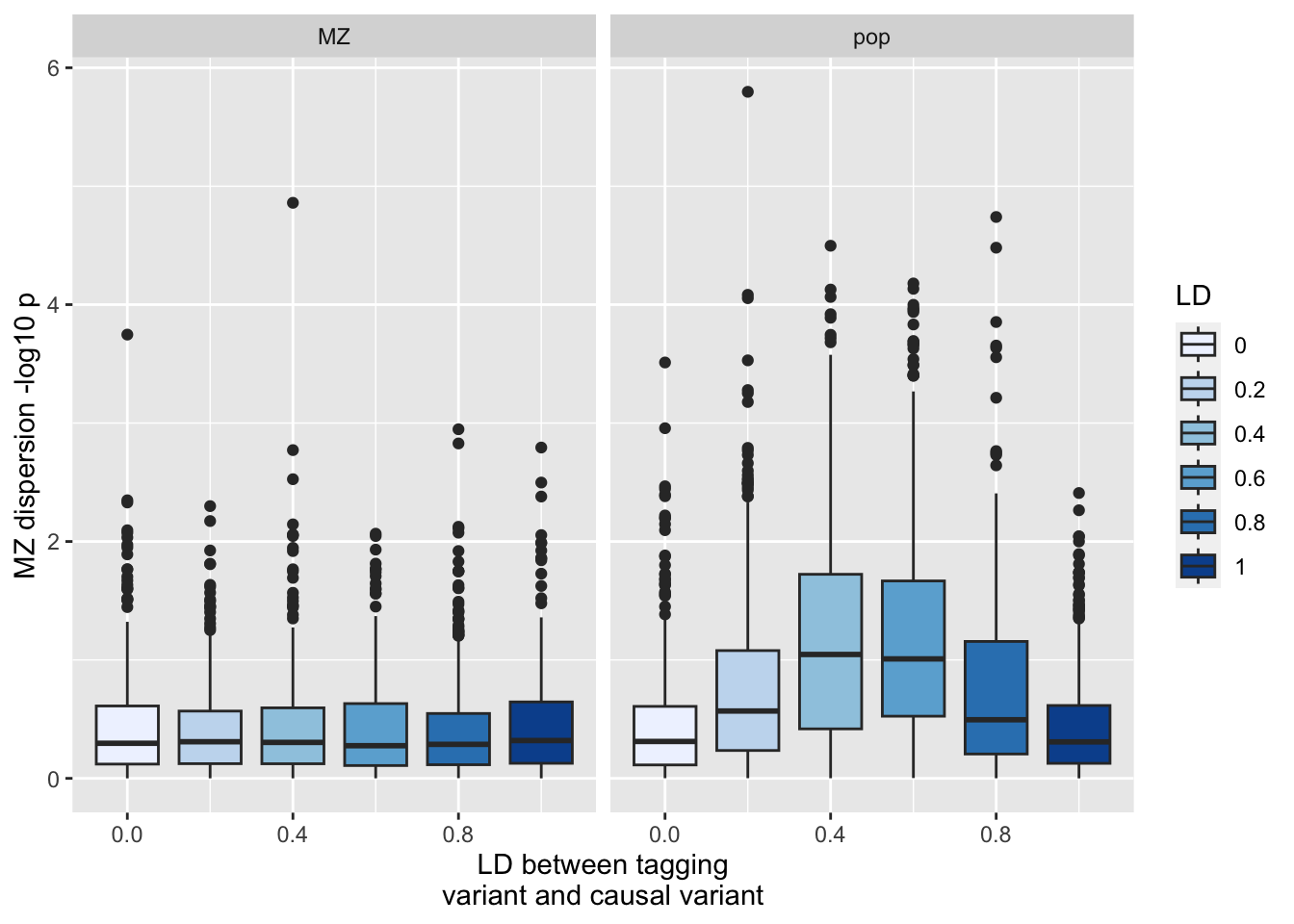
%>% :: select (r1, MZ= mz2, pop= drm2) %>% gather (., "key" , "value" , MZ, pop) %>% ggplot (., aes (x= r1, y= - log10 (value))) + geom_boxplot (aes (fill= as.factor (r1))) + scale_fill_brewer (type= "seq" ) + facet_grid (. ~ key) + labs (y= "MZ dispersion -log10 p" , x= "LD between tagging \n variant and causal variant" , fill= "LD" )
Summary
Using MZs is better powered than populations given equal sample sizes especially when h2 is large, but population sample sizes can be much larger which outweighs the power advantage of MZs
MZs restricted to GxE or true variance heterogeneity (no GxG)
MZs not liable to the LD leakage issue
Using DZs at loci where IBD=1 is possible which could boost power
Could expand DZ model to all loci but would need to generate model appropriately.
R version 4.2.1 Patched (2022-09-06 r82817)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.6.2
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRlapack.dylib
locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] simulateGP_0.1.2 tidyr_1.2.1 ggplot2_3.4.0 dplyr_1.0.10
loaded via a namespace (and not attached):
[1] RColorBrewer_1.1-3 pillar_1.8.1 compiler_4.2.1 tools_4.2.1
[5] digest_0.6.31 jsonlite_1.8.4 evaluate_0.19 lifecycle_1.0.3
[9] tibble_3.1.8 gtable_0.3.1 pkgconfig_2.0.3 rlang_1.0.6
[13] DBI_1.1.3 cli_3.5.0 yaml_2.3.6 xfun_0.36
[17] fastmap_1.1.0 withr_2.5.0 stringr_1.5.0 knitr_1.41
[21] generics_0.1.3 vctrs_0.5.1 htmlwidgets_1.5.4 grid_4.2.1
[25] tidyselect_1.2.0 glue_1.6.2 R6_2.5.1 fansi_1.0.3
[29] rmarkdown_2.16 farver_2.1.1 purrr_1.0.0 magrittr_2.0.3
[33] ellipsis_0.3.2 scales_1.2.1 htmltools_0.5.4 assertthat_0.2.1
[37] colorspace_2.0-3 labeling_0.4.2 utf8_1.2.2 stringi_1.7.8
[41] munsell_0.5.0