Can winner’s curse generate a high conditional F statistic

Background

Multivariable MR requires that exposure effects are heterogeneous, indicated by the conditional F-statistic. If the sample overlap between two exposures is 0, how much can winner’s curse drive apparent heterogeneity?

library(simulateGP)
library(dplyr)
library(MVMR)
library(ggplot2)

# 1. Simulate architecture for nsnps
# 2. Simualate two independent GWAS summary datasets each with sample size nid
# 3. Identify instruments significant in each dataset
# 4. Calculate conditional Fstat for these independent instruments
# 5. Repeat for a random selection of instruments (no selection)
sim <- function(nsnp, nid)
{
    map <- tibble(snp=1:nsnp, af=runif(nsnp, 0.01, 0.99)) %>%
        generate_gwas_params(h2=0.4, S=-0.1, Pi=1)
    map

    ss1 <- generate_gwas_ss(map, nid)
    ss2 <- generate_gwas_ss(map, nid)

    table(ss1$pval < 5e-8, ss2$pval < 5e-8)

    inst1 <- subset(ss1, pval < 5e-8)$snp
    inst2 <- subset(ss2, pval < 5e-8)$snp
    insts <- unique(c(inst1, inst2))

    mvmrdat <- format_mvmr(
        BXGs = cbind(ss1$bhat[insts], ss2$bhat[insts]), 
        BYG = runif(length(insts)), 
        seBXGs = cbind(ss1$se[insts], ss2$se[insts]),
        seBYG = rep(0.1, length(insts)),
        RSID = insts
    )
    selected <- strength_mvmr(mvmrdat, 0)

    insts_random <- sample(map$snp, length(insts), replace=FALSE)
    mvmrdat_random <- format_mvmr(
        BXGs = cbind(ss1$bhat[insts_random], ss2$bhat[insts_random]), 
        BYG = runif(length(insts_random)), 
        seBXGs = cbind(ss1$se[insts_random], ss2$se[insts_random]),
        seBYG = rep(0.1, length(insts_random)),
        RSID = insts
    )    
    random <- strength_mvmr(mvmrdat_random, 0)
    return(list(selected=selected, random=random, ninst=length(insts)))
}

# Simulation parameters
param <- expand.grid(
    nsnp=seq(5000, 100000, by=5000), 
    nid=240000,
    nsim=1:5
)

# Run simulations
o <- lapply(1:nrow(param), function(i)
{
    x <- param[i,]
    o <- sim(x$nsnp, x$nid)
    bind_cols(
        x, 
        tibble(
            what=c("selected", "random"), 
            Fstat=c(o$selected$exposure1[1], o$random$exposure1[1]), 
            ninst=o$ninst
        )
    )
}) %>% bind_rows()

# Plot
ggplot(o, aes(x=as.factor(nsnp), y=Fstat)) +
geom_boxplot(aes(fill=what)) +
labs(x="Number of causal variants", y="Conditional F-statistic", fill="") +
theme(axis.text.x=element_text(angle=90))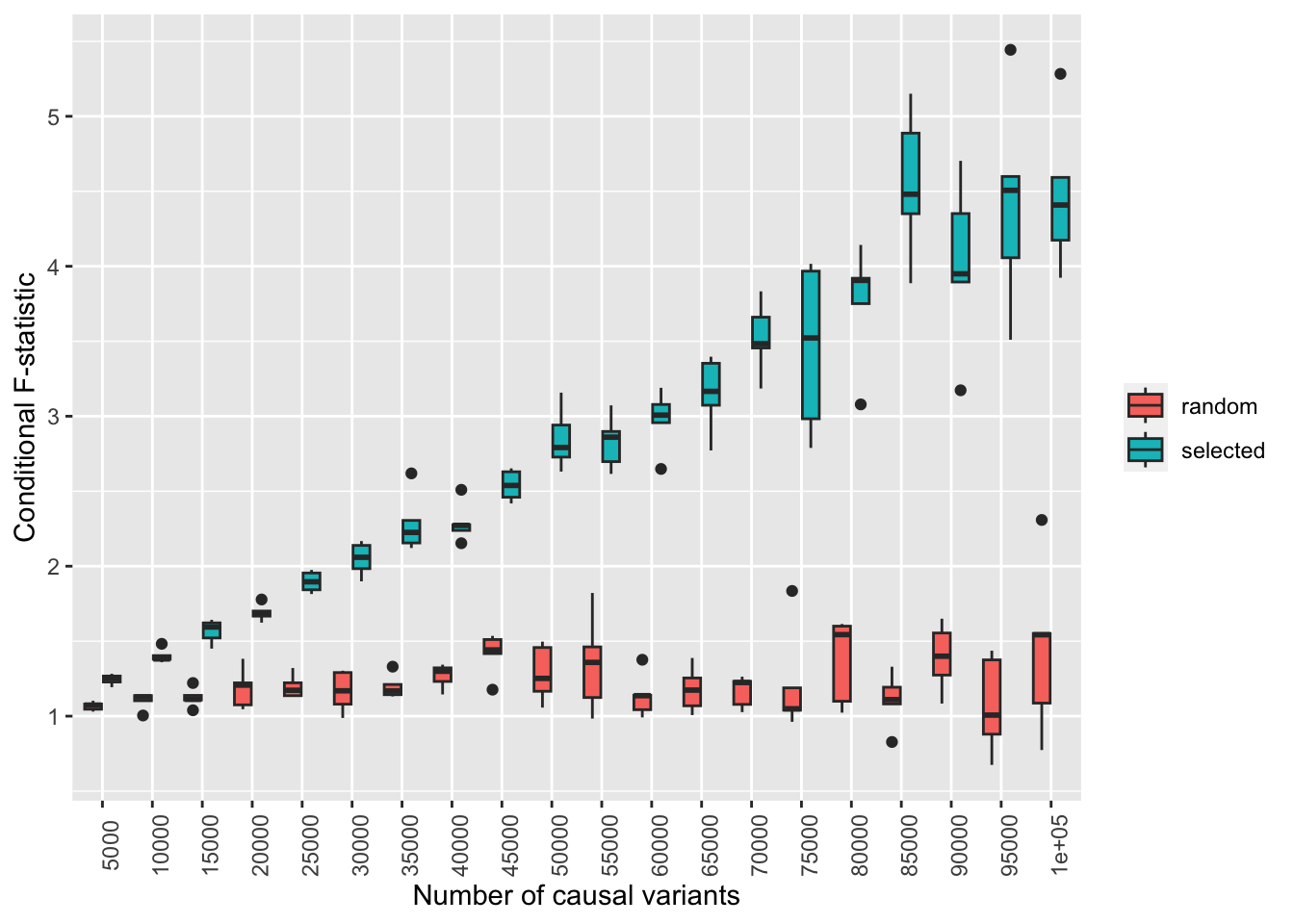

So, it looks like winner’s curse alone can generate quite large conditional F stat ~4 under some circumstances - that the number of causal variants is very high like 60k with n=240000 in each GWAS (which essentially means that most of the GWAS hits are hovering around the significance threshold, which is where winner’s curse is maximised). The empirical analysis in ukbb will be useful to get a more concrete answer on how much it’s realistically contributing

---

sessionInfo()