Convert Bayes factors to beta and standard error

statistics
fine mapping
Author

Gibran Hemani

Published

January 26, 2023

Background

Is it possible to convert BF to beta and standard error? According to Giambartolomei et al 2014 -

\[ ABF = \sqrt{1-r} \times exp(rZ^2/2) \]

so

\[ |Z| = \sqrt{\frac{2 * log(ABF) - log(\sqrt{1-r})}{r}} \]

here \(r = W / V\) where V is the variance of the SNP effect estimate

\[ V \approx \frac{1}{2np(1-p)} \]

where n is sample size and p is allele frequency (assumes small amount of variance explained in trait and sd of trait is 1).

Run simulation

  1. Use regional LD matrix to generate summary statistics with a single causal variant
  2. Use SuSiE to perform fine mapping
  3. Convert SuSiE Bayes Factors into Z scores, betas, standard errors
  4. Compare converted Z, beta, se against original simulated Z, beta, SE

Simulation

Libraries

library(simulateGP)
library(susieR)
library(here)
here() starts at /Users/gh13047/repo/lab-book
library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

Conversion function for logBF to z, beta, se

#' Convert log Bayes Factor to summary stats
#'
#' @param lbf p-vector of log Bayes Factors for each SNP
#' @param n Overall sample size
#' @param af p-vector of allele frequencies for each SNP
#' @param prior_v Variance of prior distribution. SuSiE uses 50
#'
#' @return tibble with lbf, af, beta, se, z
lbf_to_z_cont <- function(lbf, n, af, prior_v=50)
{
  se = sqrt(1 / (2 * n * af * (1-af)))
  r = prior_v / (prior_v + se^2)
  z = sqrt((2 * lbf - log(sqrt(1-r)))/r)
  beta <- z * se
  return(tibble(lbf, af, z, beta, se))
}

Read in example LD matrix from simulateGP repository

map <- readRDS(url("https://github.com/explodecomputer/simulateGP/raw/master/data/ldobj_5_141345062_141478055.rds", "rb"))
glimpse(map)
List of 3
 $ ld  : num [1:501, 1:501] 1 0.565 0.566 0.565 0.565 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:501] "V2000" "V2001" "V2002" "V2003" ...
 $ map : tibble [501 × 6] (S3: tbl_df/tbl/data.frame)
  ..$ chr: int [1:501] 5 5 5 5 5 5 5 5 5 5 ...
  ..$ snp: chr [1:501] "rs252141" "rs252140" "rs252139" "rs187544" ...
  ..$ pos: int [1:501] 141345062 141345192 141345218 141345361 141345678 141345805 141346830 141347360 141347465 141347931 ...
  ..$ alt: chr [1:501] "T" "T" "C" "G" ...
  ..$ ref: chr [1:501] "C" "C" "T" "T" ...
  ..$ af : num [1:501] 0.627 0.831 0.83 0.831 0.831 ...
  ..- attr(*, ".internal.selfref")=<externalptr> 
 $ nref: num 503

Generate summary statistics for a single causal variant and

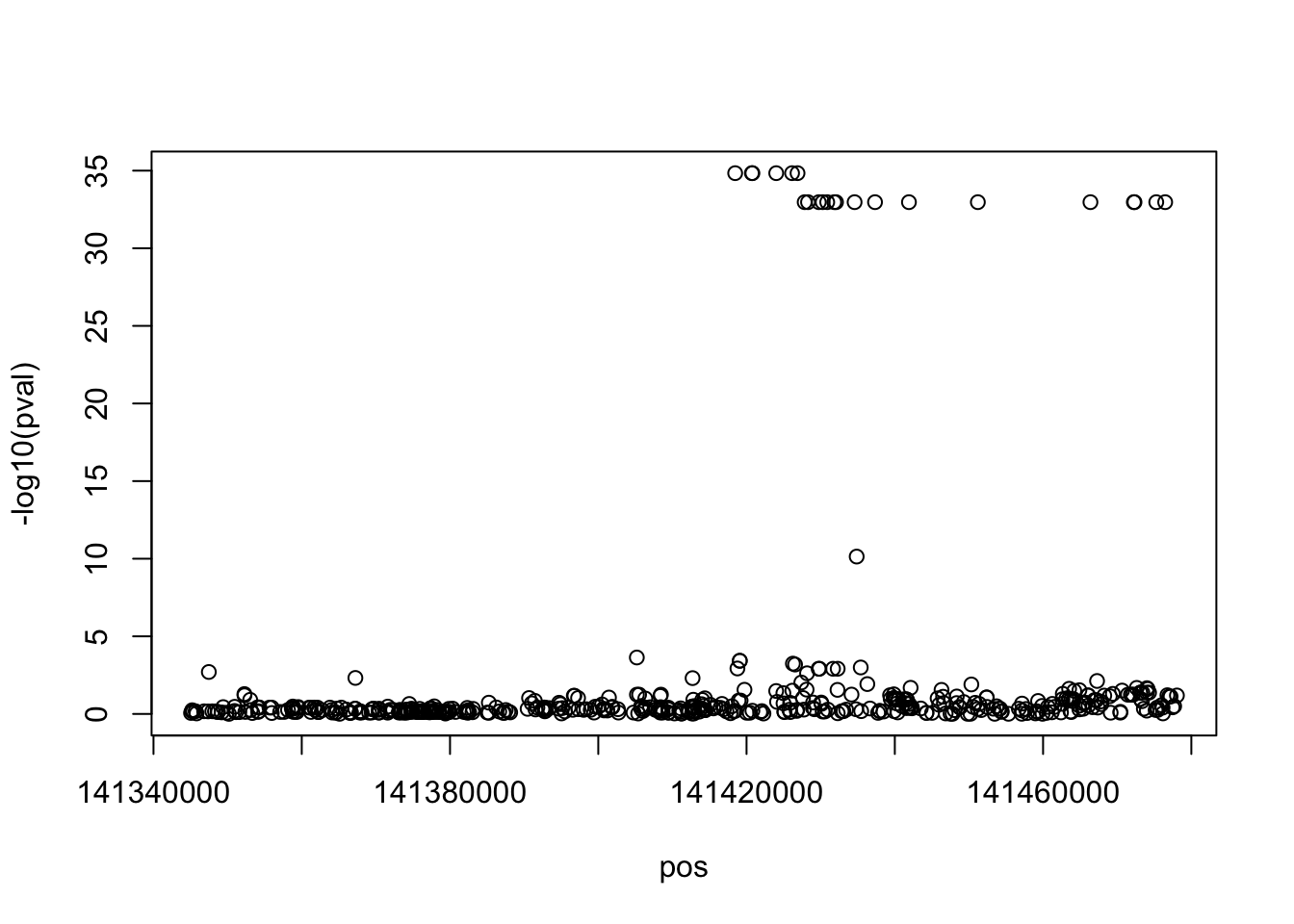
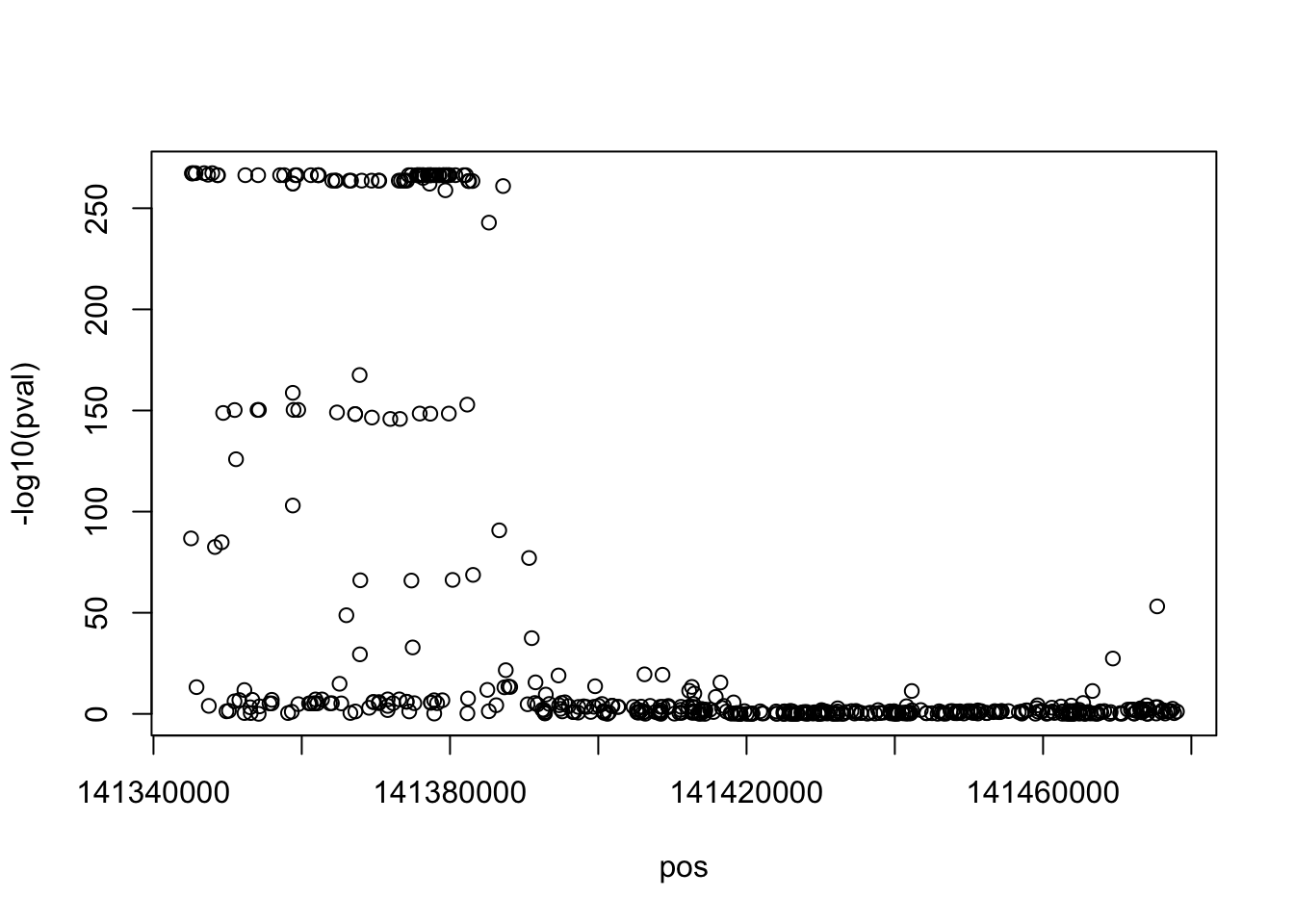
set.seed(1234)
ss <- map$map %>%
    generate_gwas_params(h2=0.003, Pi=1/nrow(.)) %>%
    generate_gwas_ss(50000, ld=map$ld)
table(ss$beta == 0)

FALSE  TRUE 
    1   500 
plot(-log10(pval) ~ pos, ss)

Run SuSiE

sout <- susie_rss(ss$bhat / ss$se, R = map$ld, n = 50000, bhat = ss$bhat, var_y=1)
WARNING: XtX is not symmetric; forcing XtX to be symmetric by replacing XtX with (XtX + t(XtX))/2
summary(sout)

Variables in credible sets:

 variable variable_prob cs
      286     0.1604616  1
      306     0.1604616  1
      291     0.1604616  1
      300     0.1604616  1
      274     0.1604616  1
      284     0.1604616  1

Credible sets summary:

 cs cs_log10bf cs_avg_r2 cs_min_r2                variable
  1   30.37357         1         1 274,284,286,291,300,306
glimpse(sout)
List of 18
 $ alpha                 : num [1:10, 1:501] 6.9e-35 2.0e-03 2.0e-03 2.0e-03 2.0e-03 ...
 $ mu                    : num [1:10, 1:501] 0.000761 0 0 0 0 ...
 $ mu2                   : num [1:10, 1:501] 2.04e-05 0.00 0.00 0.00 0.00 ...
 $ KL                    : num [1:10] 6.75 -1.24e-14 -1.24e-14 -1.24e-14 -1.24e-14 ...
 $ lbf                   : num [1:10] 6.99e+01 1.24e-14 1.24e-14 1.24e-14 1.24e-14 ...
 $ lbf_variable          : num [1:10, 1:501] -2.51 0 0 0 0 ...
 $ sigma2                : num 1
 $ V                     : num [1:10] 0.00307 0 0 0 0 ...
 $ pi                    : num [1:501] 0.002 0.002 0.002 0.002 0.002 ...
 $ null_index            : num 0
 $ XtXr                  : num [1:501, 1] -0.328 70.558 72.085 70.558 70.558 ...
 $ converged             : logi TRUE
 $ elbo                  : num [1:2] -70876 -70876
 $ niter                 : int 2
 $ X_column_scale_factors: num [1:501] 1 1 1 1 1 1 1 1 1 1 ...
 $ intercept             : num NA
 $ sets                  :List of 5
  ..$ cs                :List of 1
  .. ..$ L1: int [1:6] 274 284 286 291 300 306
  ..$ purity            :'data.frame':  1 obs. of  3 variables:
  .. ..$ min.abs.corr   : num 1
  .. ..$ mean.abs.corr  : num 1
  .. ..$ median.abs.corr: num 1
  ..$ cs_index          : int 1
  ..$ coverage          : num 0.963
  ..$ requested_coverage: num 0.95
 $ pip                   : num [1:501] 0 0 0 0 0 0 0 0 0 0 ...
 - attr(*, "class")= chr "susie"

Get Z scores from lbf

a <- lbf_to_z_cont(sout$lbf_variable[1,], 50000, ss$af, prior_v = 50)
a
# A tibble: 501 × 5
     lbf     af     z    beta      se
   <dbl>  <dbl> <dbl>   <dbl>   <dbl>
 1 -2.51 0.373   1.41 0.00919 0.00654
 2 -2.43 0.169   1.37 0.0115  0.00844
 3 -2.37 0.17    1.42 0.0119  0.00842
 4 -2.43 0.169   1.37 0.0115  0.00844
 5 -2.43 0.169   1.37 0.0115  0.00844
 6 -2.52 0.191   1.32 0.0106  0.00805
 7 -2.43 0.169   1.37 0.0115  0.00844
 8 -2.44 0.17    1.36 0.0115  0.00842
 9  2.23 0.0139  3.17 0.0855  0.0270 
10 -2.43 0.169   1.37 0.0115  0.00844
# … with 491 more rows

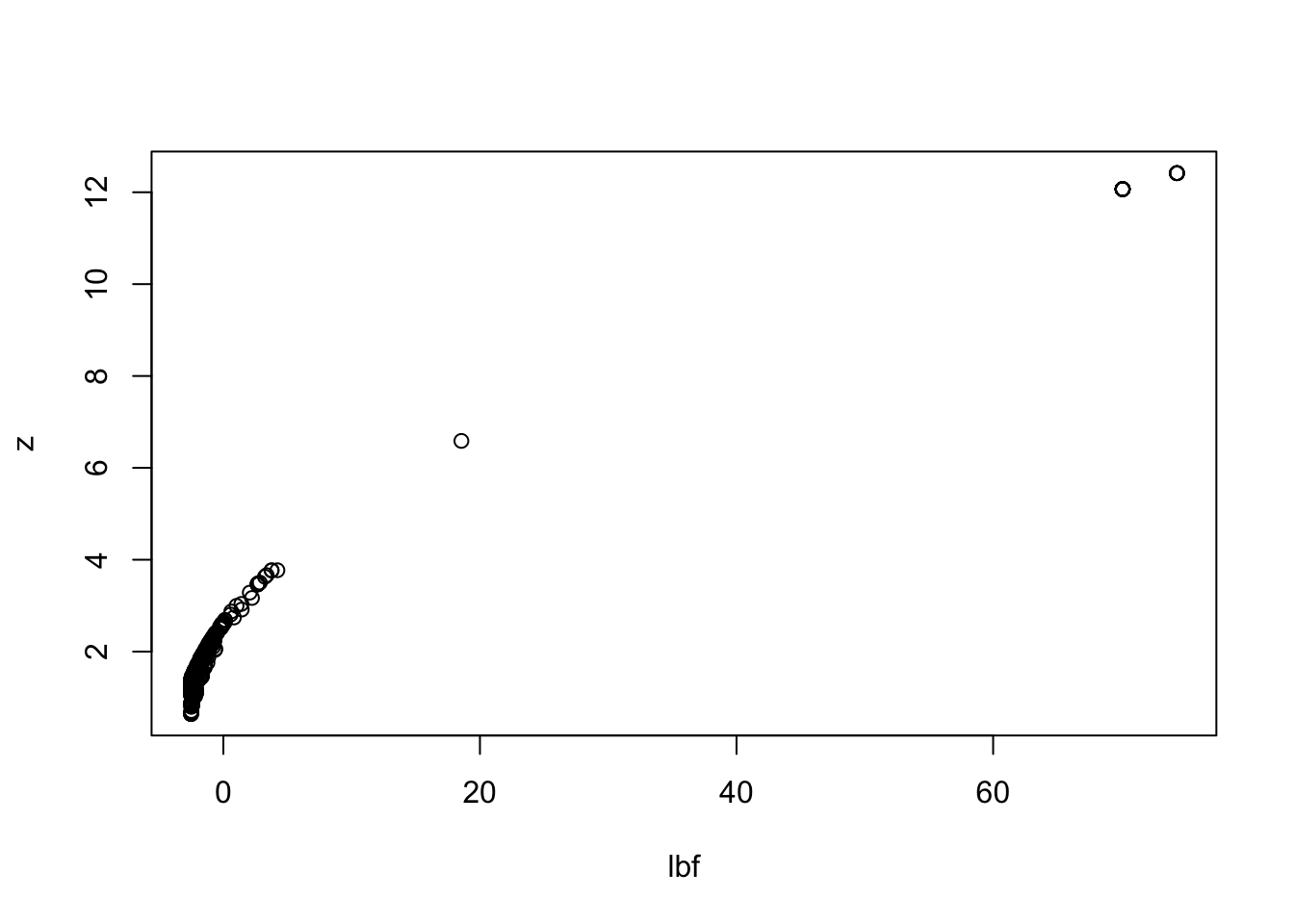
Relationship between lbf and re-estimated z

plot(z ~ lbf, a)

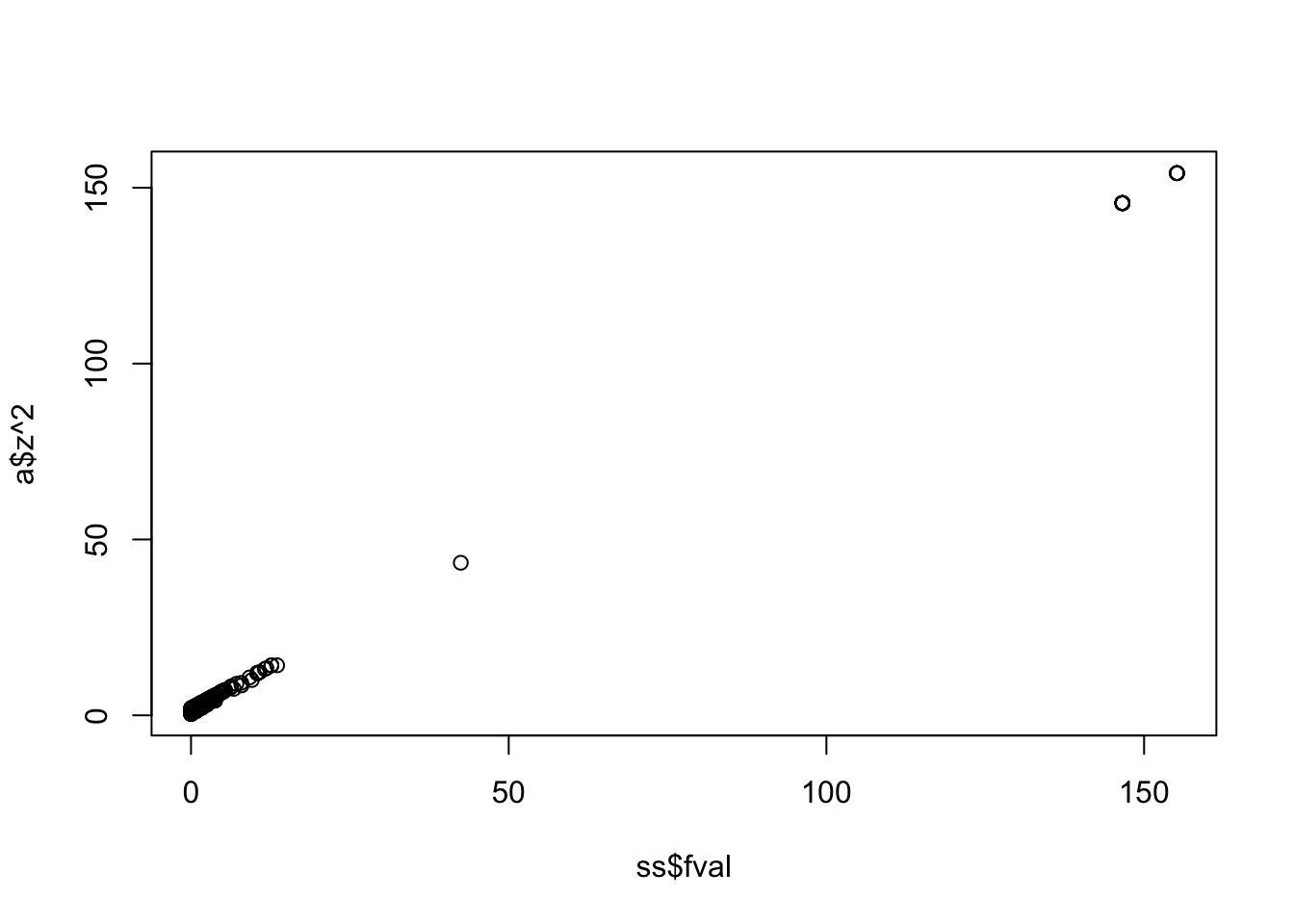
New Z vs original Z

plot(a$z^2 ~ ss$fval)

lm(a$z^2 ~ ss$fval)

Call:
lm(formula = a$z^2 ~ ss$fval)

Coefficients:
(Intercept)      ss$fval  
     1.5141       0.9834

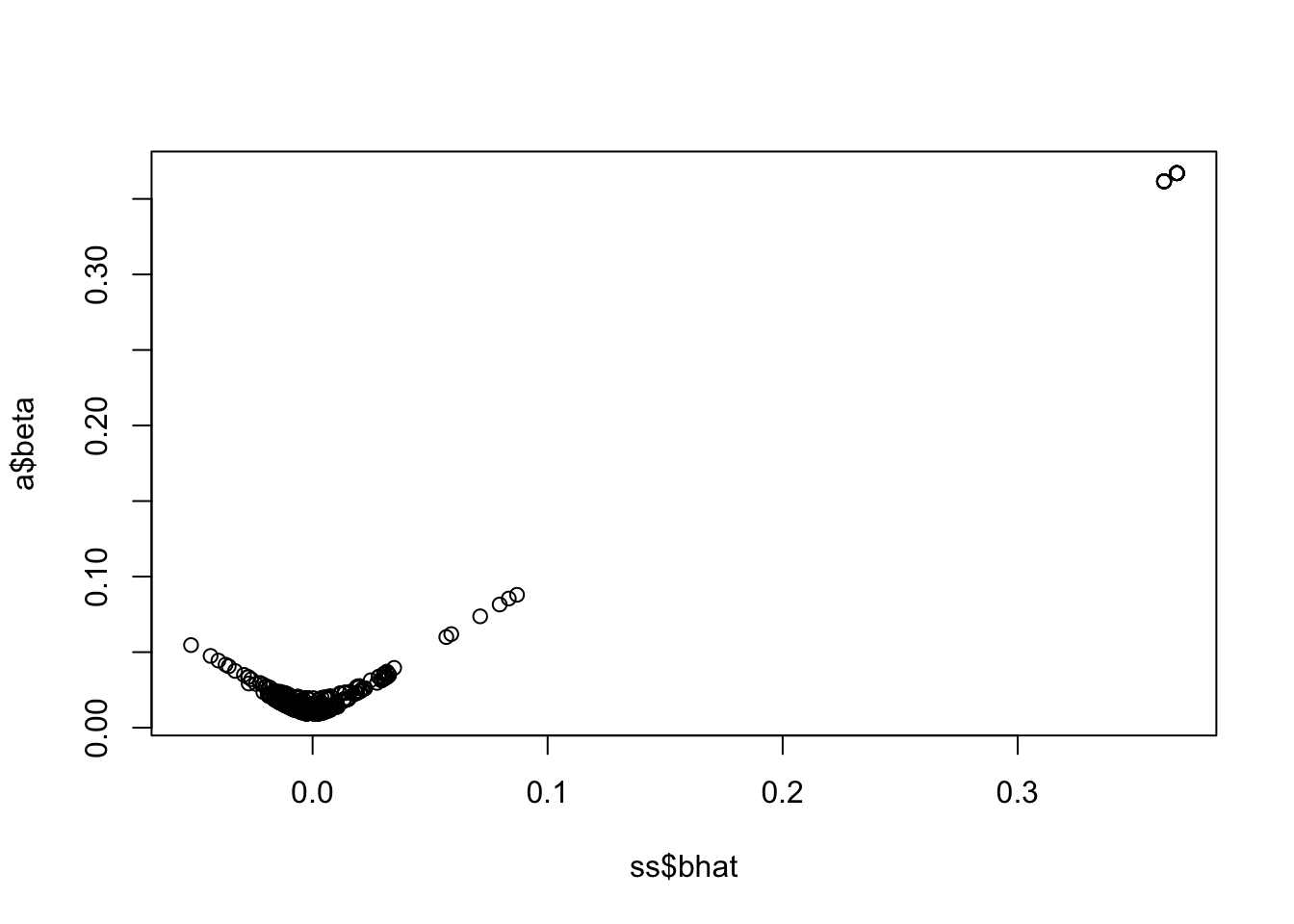
New beta vs original beta

plot(a$beta ~ ss$bhat)

Two causal variants

Set two causal variants at either end of the region

set.seed(12)
param <- map$map
param$beta <- 0
param$beta[c(10, 490)] <- 0.3
ss <- generate_gwas_ss(param, 50000, ld=map$ld)
plot(-log10(pval) ~ pos, ss)

First variant

sout <- susie_rss(ss$bhat / ss$se, R = map$ld, n = 50000, bhat = ss$bhat, var_y=1)
WARNING: XtX is not symmetric; forcing XtX to be symmetric by replacing XtX with (XtX + t(XtX))/2
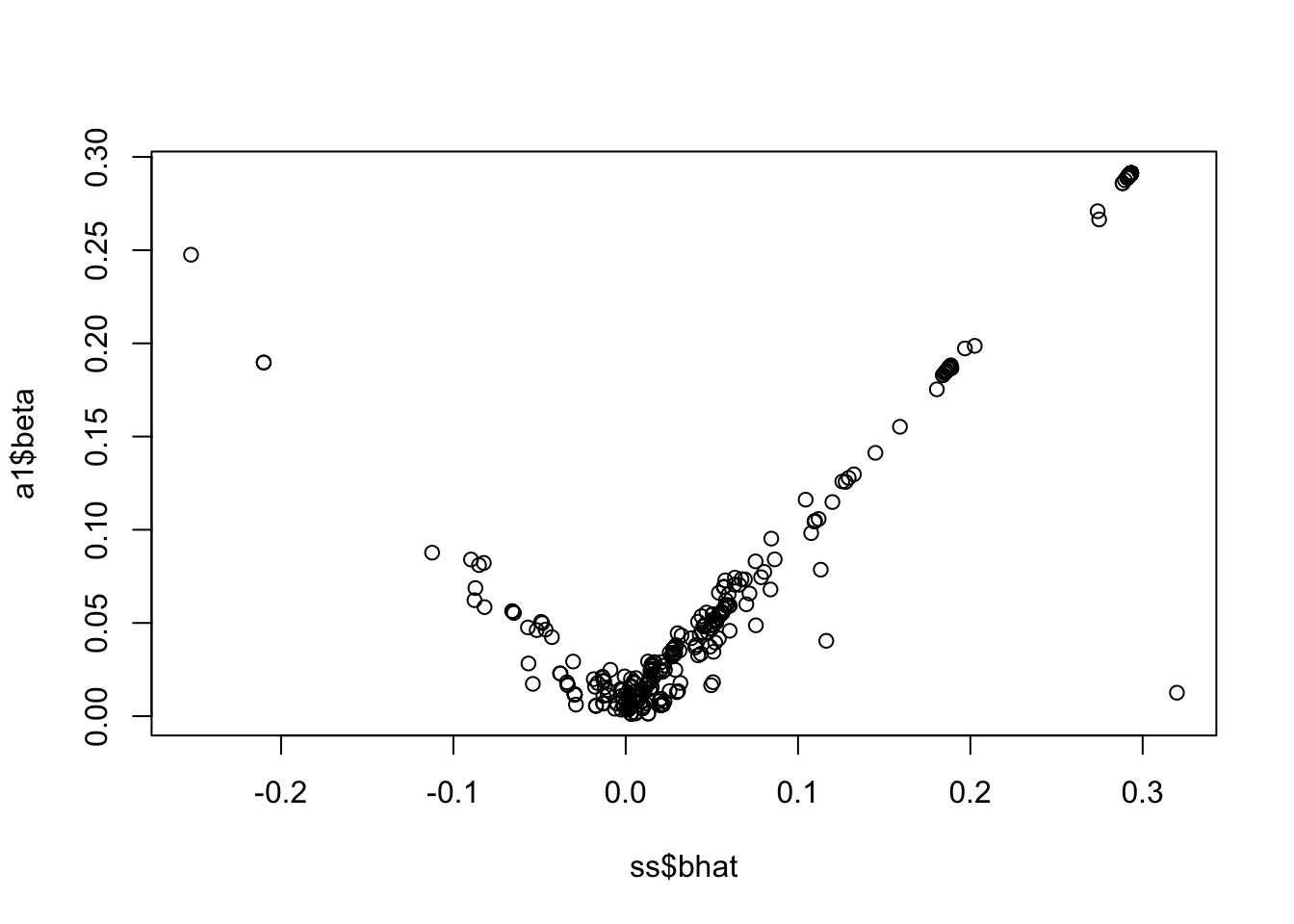
a1 <- lbf_to_z_cont(sout$lbf_variable[1,], 50000, ss$af, prior_v = 50)
Warning in sqrt((2 * lbf - log(sqrt(1 - r)))/r): NaNs produced
plot(a1$beta ~ ss$bhat)

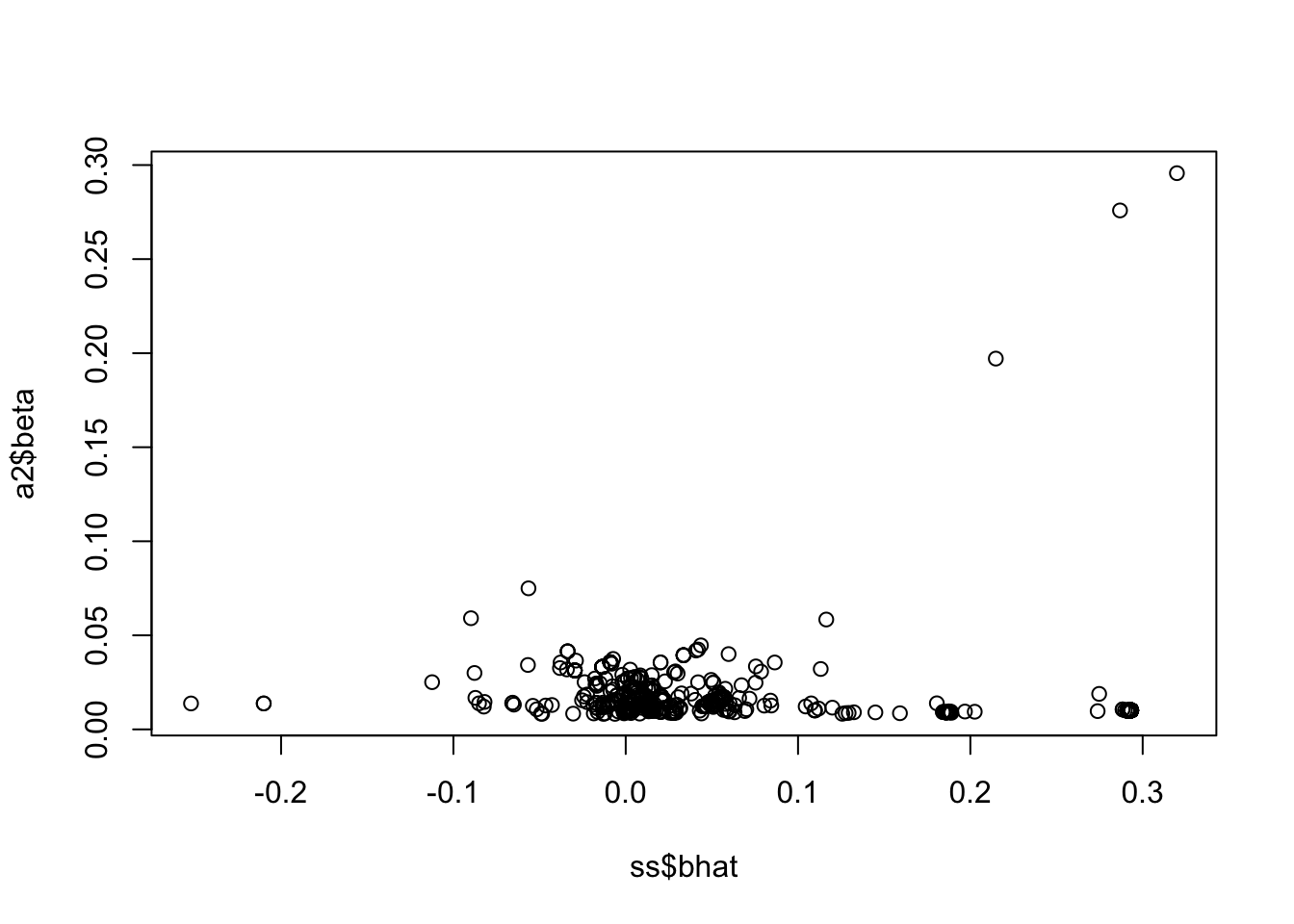
a2 <- lbf_to_z_cont(sout$lbf_variable[2,], 50000, ss$af, prior_v = 50)
plot(a2$beta ~ ss$bhat)

This looks good - it’s setting different values to 0 in the two lbf vectors that correspond to two causal variants

sessionInfo()
R version 4.2.1 Patched (2022-09-06 r82817)
Platform: aarch64-apple-darwin20 (64-bit)
Running under: macOS Monterey 12.6.2

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.2-arm64/Resources/lib/libRlapack.dylib

locale:
[1] en_GB.UTF-8/en_GB.UTF-8/en_GB.UTF-8/C/en_GB.UTF-8/en_GB.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] dplyr_1.0.10     here_1.0.1       susieR_0.12.27   simulateGP_0.1.2

loaded via a namespace (and not attached):
 [1] Rcpp_1.0.9         plyr_1.8.7         compiler_4.2.1     pillar_1.8.1      
 [5] tools_4.2.1        digest_0.6.31      jsonlite_1.8.4     evaluate_0.19     
 [9] lifecycle_1.0.3    tibble_3.1.8       gtable_0.3.1       lattice_0.20-45   
[13] pkgconfig_2.0.3    rlang_1.0.6        Matrix_1.4-1       DBI_1.1.3         
[17] cli_3.5.0          yaml_2.3.6         xfun_0.36          fastmap_1.1.0     
[21] stringr_1.5.0      knitr_1.41         generics_0.1.3     vctrs_0.5.1       
[25] htmlwidgets_1.5.4  rprojroot_2.0.3    tidyselect_1.2.0   grid_4.2.1        
[29] reshape_0.8.9      glue_1.6.2         R6_2.5.1           fansi_1.0.3       
[33] rmarkdown_2.16     mixsqp_0.3-48      irlba_2.3.5.1      ggplot2_3.4.0     
[37] magrittr_2.0.3     MASS_7.3-58.1      matrixStats_0.63.0 scales_1.2.1      
[41] htmltools_0.5.4    assertthat_0.2.1   colorspace_2.0-3   utf8_1.2.2        
[45] stringi_1.7.8      munsell_0.5.0      crayon_1.5.2